
【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.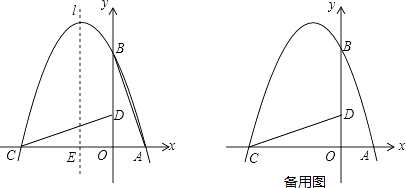
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
【答案】
(1)解:在Rt△AOB中,OA=1,tan∠BAO= ![]() =3,
=3,
∴OB=3OA=3.
∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,
∴△DOC≌△AOB,
∴OC=OB=3,OD=OA=1,
∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).
代入解析式为
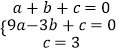 ,
,
解得: 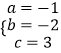 .
.
∴抛物线的解析式为y=﹣x2﹣2x+3
(2)解:①∵抛物线的解析式为y=﹣x2﹣2x+3,
∴对称轴l=﹣ ![]() =﹣1,
=﹣1,
∴E点的坐标为(﹣1,0).
如图, 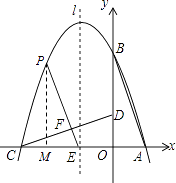
当∠CEF=90°时,△CEF∽△COD.此时点P在对称轴上,即点P为抛物线的顶点,P(﹣1,4);
当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP.
∴ ![]() ,
,
∴MP=3EM.
∵P的横坐标为t,
∴P(t,﹣t2﹣2t+3).
∵P在第二象限,
∴PM=﹣t2﹣2t+3,EM=﹣1﹣t,
∴﹣t2﹣2t+3=﹣(t﹣1)(t+3),
解得:t1=﹣2,t2=﹣3(因为P与C重合,所以舍去),
∴t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3.
∴P(﹣2,3).
∴当△CEF与△COD相似时,P点的坐标为:(﹣1,4)或(﹣2,3);
②设直线CD的解析式为y=kx+b,由题意,得
![]() ,
,
解得: ![]() ,
,
∴直线CD的解析式为:y= ![]() x+1.
x+1.
设PM与CD的交点为N,则点N的坐标为(t, ![]() t+1),
t+1),
∴NM= ![]() t+1.
t+1.
∴PN=PM﹣NM=﹣t2﹣2t+3﹣( ![]() t+1)=﹣t2﹣
t+1)=﹣t2﹣ ![]() +2.
+2.
∵S△PCD=S△PCN+S△PDN,
∴S△PCD= ![]() PNCM+
PNCM+ ![]() PNOM
PNOM
= ![]() PN(CM+OM)
PN(CM+OM)
= ![]() PNOC
PNOC
= ![]() ×3(﹣t2﹣
×3(﹣t2﹣ ![]() +2)
+2)
=﹣ ![]() (t+
(t+ ![]() )
)![]() ,
,
∴当t=﹣ ![]() 时,S△PCD的最大值为
时,S△PCD的最大值为 ![]() .
.
【解析】(1)先求出A、B、C的坐标,再用待定系数法就可以直接求出二次函数的解析式;(2)①抛物线的解析式为y=﹣x2﹣2x+3,故可以求出抛物线的对称轴,分类讨论当∠CEF=90°时,△CEF∽△COD.此时点P在对称轴上,即点P为抛物线的顶点,当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP.根据相似三角形的性质即可求出P点的坐标;②设直线CD的解析式为y=kx+b,由待定系数法即可求出解析式,设PM与CD的交点为N,根据CD的解析式表示出点N的坐标,再根据S△PCD=S△PCN+S△PDN,就可以表示出△PCD的面积,利用顶点式就可以求出结论。
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如下图时用黑色的正六边形和白色的正方形按照一定的规律组合而成的两色图案

(1)当黑色的正六边形的块数为1时,有6块白色的正方形配套;当黑色的正六边形块数为2时,有11块白色的正方形配套;则当黑色的正六边形块数为3,10时,分别写出白色的正方形配套块数;
(2)当白色的正方形块数为201时,求黑色的正六边形的块数.
(3)组成白色的正方形的块数能否为100,如果能,求出黑色的正六边形的块数,如果不能,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y= ![]() ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.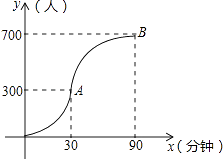
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,MN,EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:
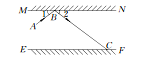
(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
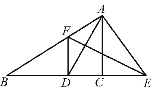
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线分别交AB于点F,交BC的延长线于点E.
求证:(1)∠EAD=∠EDA;
(2)DF∥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A:(1,0).A![]() (1,-1),A
(1,-1),A![]() (-1,-l).A
(-1,-l).A![]() (-1, 1), A
(-1, 1), A![]() (2, 1),...则点A
(2, 1),...则点A![]() 的坐标是( )
的坐标是( )
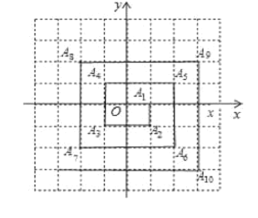
A.(506,505)B.(-505,-505)C.(505,-505)D.(-505,505)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com