
【题目】平面直角坐标系中,点A、B坐标分别为(0,4)、(2,0),点C为直线AB上一点,若BC=3AC,则点C的坐标为_____.

科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF,若∠ABE=25°,则∠EFC'的度数为( )
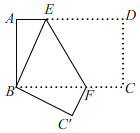
A.122.5°B.130°C.135°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为t s,当t=时,△CPQ与△CBA相似.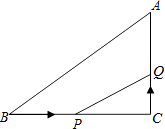
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100个,付款总额不得超过11815元.已知:厂家两种球的批发价如(表![]() )、商场在某两天的零售信息如(表
)、商场在某两天的零售信息如(表![]() ):
):
品名 | 厂家批发价(元/个) |
篮球 | 130 |
排球 | 100 |
(表![]() )
)
篮球(个) | 排球(个) | 零售总价(元) | |
第一天 | 8 | 5 | 1880 |
第二天 | 6 | 10 | 2160 |
(表![]() )
)
请解决以下问题:
(1)求出体育商场出售篮球和排球的零售单价.
(2)该采购员最多可从厂家购进篮球多少个.
(3)若该商场把这100个球全部以零售价售出,为使商场的利润不低于2580元,则采购员采购的方案有哪几种?该商场最多可盈利__________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,且抛物线的对称轴为直线x=4.
(1)求出抛物线与x轴的两个交点A,B的坐标.
(2)试确定抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:a*b=![]() ,则下列等式中对于任意实数 a、b、c 都成立的是( )
,则下列等式中对于任意实数 a、b、c 都成立的是( )
①a+(b*c)=(a+b)*(a+c) ②a*(b+c)=(a+b)*c
③a*(b+c)=(a*b)+(a*c) ④(a*b)+c= ![]() +(b*2c)
+(b*2c)
A. ①②③ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.
(1)求此抛物线的解析式;
(2)若点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,设点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.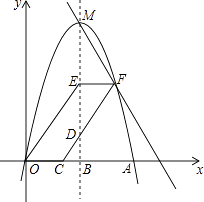
(1)求a的值及M的坐标;
(2)当BD为何值时,点F恰好落在该抛物线上?
(3)当∠DCB=45°时:
①求直线MF的解析式;
②延长OE交FM于点G,四边形DEGF和四边形OEDC的面积分别记为S1、S2 , 则S1:S2的值为(直接写答案)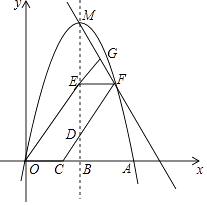
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.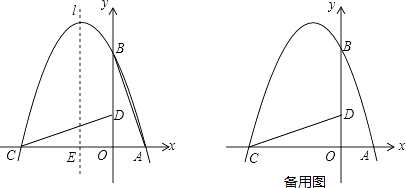
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com