
【题目】如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF,若∠ABE=25°,则∠EFC'的度数为( )
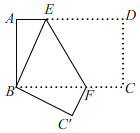
A.122.5°B.130°C.135°D.140°
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.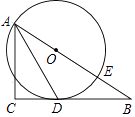
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在数轴上A,B两点对应的数分别是6,-6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF=_______;
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
①当t=1时,α=_______
②猜想∠BCE和α的数量关系,并证明;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α-β|=40°,请直接写出t的值为

查看答案和解析>>
科目:初中数学 来源: 题型:
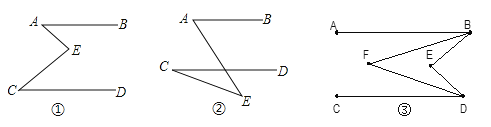
【题目】(1)如图①、②,AB∥CD,你能说明∠A、∠E、∠C的关系吗?(请在图形下的横线上写出其关系并选一个进行说明)
(2)如图③若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80,则∠BFD=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 、
、![]() 的交点为
的交点为![]() ,现作如下操作:
,现作如下操作:
第一次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第二次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第三次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
…
第![]() 次操作,分别作
次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() .
.
若![]() 度,那
度,那![]() 等于__________度.
等于__________度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将方格纸中的△ABC向上平移4个单位长度,然后向右平移6个单位长度,得到△A1B1C1.
(1)画出平移后的图形;
(2)线段AA1,BB1的位置关系是______;数量关系是________.
(3)如果每个方格的边长是1,那么△ABC的面积是___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com