
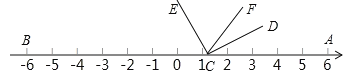
【题目】如图1,在数轴上A,B两点对应的数分别是6,-6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF=_______;
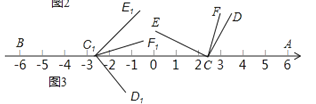
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
①当t=1时,α=_______
②猜想∠BCE和α的数量关系,并证明;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α-β|=40°,请直接写出t的值为

【答案】(1)45°;(2)①30°;②∠BCE=2α,理由见解析;(3)![]()
【解析】
(1)根据角平分线的定义计算即可;
(2)①根据∠FCD=∠ACF-∠ACD,求出∠ACF,∠ACD即可;
②猜想:∠BCE=2α.根据∠BCE=∠AOB-∠ECD-∠ACD计算即可;
(3)求出α,β(用t表示),构建方程即可解决问题;
解:(1)如图1中,

∵∠EOD=90°,OF平分∠EOD,
∴∠FOD=![]() ∠EOD=45°,
∠EOD=45°,
故答案为:45°;
(2)①如下图,
当t=1时,∵∠DCA=30°,∠ECD=90°,
∴∠ECA=120°,
∵CF平分∠ACE,
∴∠FCA=![]() ∠ECA=60°
∠ECA=60°
∴α=∠FCD=60°-30°=30°
故答案为:30°.
②如下图,猜想:∠BCE=2α.

理由:∵∠DCE=90°,∠DCF=α,
∴∠ECF=90°-α,
∵CF平分∠ACE,
∴∠ACF=∠ECF=90°-α,
∵点A,O,B共线
∴∠AOB=180°
∴∠BCE=∠AOB-∠ECD-∠ACD=180°-90°-(90°-2α)=2α.
(3)如图3中,
由题意:α=∠FCA-∠DCA=![]() (90°+30t)-30t=45°-15t,
(90°+30t)-30t=45°-15t,
β=∠AC1D1+∠AC1F1=30t+![]() (90°-30t)=45°+15t,
(90°-30t)=45°+15t,
∵β-α=40°,
∴30t=40°,
解得:t=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知ABCD的对角线AC,BD相交于点O,EF经过点O,分别交AD,BC于点E,F,且OE=4,AB=5,BC=9,则四边形ABFE的周长是( )
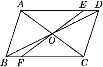
A. 13 B. 16 C. 22 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AD⊥BC,垂足为点 D,EF⊥BC,垂足为点 F,∠1+∠2=180°, 请填写∠CGD=∠CAB 的理由.

解:因为 AD⊥BC,EF⊥BC( )
所以∠ADC=90°,∠EFD=90°( )
得∠ADC=∠EFD( )
所以 AD//EF( )
得∠2+∠3=180° ( )
又因为∠1+∠2=180°(已知)
所以∠1=∠3( )
所以 DG//AB( )
所以∠CGD=∠CAB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,若四边形ABCD为“可分四边形”,∠DAB为“可分角”,且∠DCB=∠DAB,则∠DAB=°.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C. 若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了备战初三物理、化学实验操作考试.某校对初三学生进行了模拟训练.物理、化学各有4个不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定.小张同学对物理的①、②和化学的b、c实验准备得较好,请用树形图或列表法求他两科都抽到准备得较好的实验题目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF,若∠ABE=25°,则∠EFC'的度数为( )
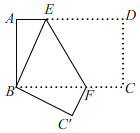
A.122.5°B.130°C.135°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
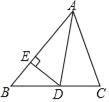
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100个,付款总额不得超过11815元.已知:厂家两种球的批发价如(表![]() )、商场在某两天的零售信息如(表
)、商场在某两天的零售信息如(表![]() ):
):
品名 | 厂家批发价(元/个) |
篮球 | 130 |
排球 | 100 |
(表![]() )
)
篮球(个) | 排球(个) | 零售总价(元) | |
第一天 | 8 | 5 | 1880 |
第二天 | 6 | 10 | 2160 |
(表![]() )
)
请解决以下问题:
(1)求出体育商场出售篮球和排球的零售单价.
(2)该采购员最多可从厂家购进篮球多少个.
(3)若该商场把这100个球全部以零售价售出,为使商场的利润不低于2580元,则采购员采购的方案有哪几种?该商场最多可盈利__________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com