
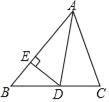
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
【答案】(1)60°;(2)27.
【解析】
(1)先求出∠BAC= 60°,再用AD是△ABC的角平分线求出∠BAD,再根据垂直,即可求解;
(2)过D作DF⊥AC于F,三角形ABC的面积为三角形ABD和三角形ACD的和即可求解.
解:(1)∵∠B=50°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,
∵AD是△ABC的角平分线,
∴∠BAD=![]() ∠BAC=
∠BAC=![]() ×60°=30°,
×60°=30°,
∵DE⊥AB,
∴∠DEA=90°,
∴∠EDA=180°﹣∠BAD﹣∠DEA=180°﹣30°﹣90°=60°;
(2)如图,过D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DF=DE=3,
又∵AB=10,AC=8,
∴S△ABC=![]() ×AB×DE+
×AB×DE+![]() ×AC×DF=
×AC×DF=![]() ×10×3+
×10×3+![]() ×8×3=27.
×8×3=27.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在数轴上A,B两点对应的数分别是6,-6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF=_______;
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
①当t=1时,α=_______
②猜想∠BCE和α的数量关系,并证明;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α-β|=40°,请直接写出t的值为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 、
、![]() 的交点为
的交点为![]() ,现作如下操作:
,现作如下操作:
第一次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第二次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第三次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
…
第![]() 次操作,分别作
次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() .
.
若![]() 度,那
度,那![]() 等于__________度.
等于__________度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将方格纸中的△ABC向上平移4个单位长度,然后向右平移6个单位长度,得到△A1B1C1.
(1)画出平移后的图形;
(2)线段AA1,BB1的位置关系是______;数量关系是________.
(3)如果每个方格的边长是1,那么△ABC的面积是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.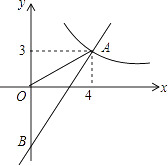
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P( ![]() +1,
+1, ![]() ﹣1)在双曲线y=
﹣1)在双曲线y= ![]() (x>0)上.
(x>0)上.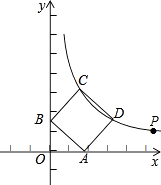
(1)求k的值;
(2)若正方形ABCD的顶点C,D在双曲线y= ![]() (x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
(x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,tan∠ABC= ![]() ,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则
,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则 ![]() 的值为( )
的值为( )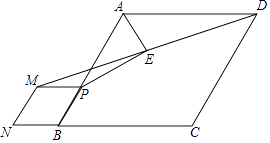
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com