
【题目】如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=ABAE.
求证:DE是⊙O的切线.
科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念。
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。
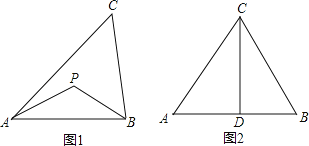
举例:如图1,若PA=PB,则点P为△ABC的准外心。
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=![]() AB,求∠APB的度数。
AB,求∠APB的度数。
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD的对角线AC,BD相交于点O,EF经过点O,分别交AD,BC于点E,F,且OE=4,AB=5,BC=9,则四边形ABFE的周长是( )
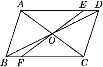
A. 13 B. 16 C. 22 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁一起研究一道数学题,如图,已知 EF⊥AB,CD⊥AB,甲说:“如果还知道∠CDG=∠BFE,则能得到∠AGD=∠ACB.”乙说:“如果还知道∠AGD=∠ACB,则能得到∠CDG=∠BFE.”丙说:“∠AGD 一定大于∠BFE.”丁说:“如果连接 GF,则 GF∥AB.”他们四人中,正确的是( )
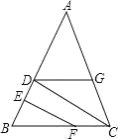
A.0 个B.1 个C.2 个D.3 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD.∠1=∠2,∠3=∠4,试说明 AD∥BE,请你将下面解答过程填写完整.

解:∵AB∥CD,
∴∠4= ( )
∵∠3=∠4
∴∠3= (等量代换)
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAE 即∠BAE= .
∴∠3= ( )
∴AD∥BE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
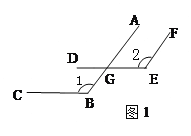
【题目】已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的数量关系,并说明你的理由.
(1)如图1,AB∥EF,BC∥DE.猜想∠1与∠2的数量关系是:_______.
(2)如图2,AB∥EF,BC∥DE. 猜想∠1与∠2的数量关系是:_______.
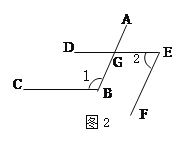
(3)由(1)(2)可以得出的结论是:如果一个角的两边与另一个角的两边分别平行,那么这两个角_____ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AD⊥BC,垂足为点 D,EF⊥BC,垂足为点 F,∠1+∠2=180°, 请填写∠CGD=∠CAB 的理由.

解:因为 AD⊥BC,EF⊥BC( )
所以∠ADC=90°,∠EFD=90°( )
得∠ADC=∠EFD( )
所以 AD//EF( )
得∠2+∠3=180° ( )
又因为∠1+∠2=180°(已知)
所以∠1=∠3( )
所以 DG//AB( )
所以∠CGD=∠CAB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,若四边形ABCD为“可分四边形”,∠DAB为“可分角”,且∠DCB=∠DAB,则∠DAB=°.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
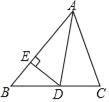
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com