
【题目】联想三角形外心的概念,我们可引入如下概念。
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。
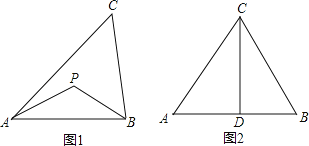
举例:如图1,若PA=PB,则点P为△ABC的准外心。
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=![]() AB,求∠APB的度数。
AB,求∠APB的度数。
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长。
【答案】∠APB=90°,PA=2或![]()
【解析】解:应用:①若PB=PC,连接PB,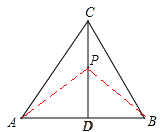
则∠PCB=∠PBC,
∵CD为等边三角形的高,∴AD=BD,∠PCB=30°。
∴∠PBD=∠PBC=30°,∴PD=![]() DB=
DB=![]() AB。
AB。
与已知PD=![]() AB矛盾,∴PB≠PC。
AB矛盾,∴PB≠PC。
②若PA=PC,连接PA,同理可得PA≠PC。
③若PA=PB,由PD=![]() AB,得PD=AD =BD,∴∠APD=∠BPD=45°。∴∠APB=90°。
AB,得PD=AD =BD,∴∠APD=∠BPD=45°。∴∠APB=90°。
探究:∵BC=5,AB=3,∴AC=![]() 。
。
①若PB=PC,设PA=![]() ,则
,则![]() ,∴
,∴![]() ,即PA=
,即PA=![]() 。
。
②若PA=PC,则PA=2。
③若PA=PB,由图知,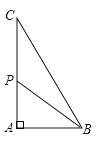
在Rt△PAB中,不可能。
∴PA=2或![]() 。
。
应用:连接PA、PB,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况利用等边三角形的性质求出PD与AB的关系,然后判断出只有情况③是合适的,再根据等腰直角三角形的性质求出∠APB=45°,然后即可求出∠APB的度数。
探究:先根据勾股定理求出AC的长度,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况,根据三角形的性质计算即可得解


科目:初中数学 来源: 题型:
【题目】以下叙述正确的有( )
①对顶角相等;②同位角相等;③两直角相等;④邻补角相等;⑤多边形的外角和都相等;⑥三角形的中线把原三角形分成面积相等的两个三角形
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在![]() ,
,![]() 两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是
两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是![]() 元,且随身听的单价比书包的单价的
元,且随身听的单价比书包的单价的![]() 倍少
倍少![]() 元.
元.
(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市![]() 所有商品打八五折销售,超市
所有商品打八五折销售,超市![]() 全场购物每满
全场购物每满![]() 元返购物券
元返购物券![]() 元销售(不足
元销售(不足![]() 元不返券,购物券全场通用),但他只带了
元不返券,购物券全场通用),但他只带了![]() 元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.则下列结论:①AD上任意一点到点C,B的距离相等;②AD上任意一点到边AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中正确的个数为( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠DAC+∠ACB=180°,EF//BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°,则∠FEC的度数是( )
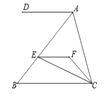
A.10°B.20°C.15°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
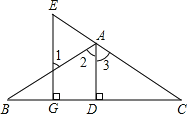
【题目】如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:AD平分∠ABC.下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC(已知)
∴∠ADC=∠EGC=90°( )
∴EG∥AD( )
∴∠E=________( )、
∠1=__________( )
又∵∠E=∠1(已知)
∴∠2=∠3( )
∴AD平分∠BAC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
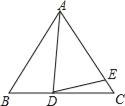
【题目】已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.
(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.
(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.
(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com