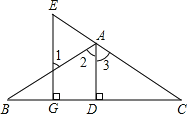
【题目】如图，已知：AD⊥BC于D，EG⊥BC于G，∠E=∠1，求证：AD平分∠ABC．下面是部分推理过程，请你将其补充完整：
∵AD⊥BC于D，EG⊥BC（已知）
∴∠ADC=∠EGC=90°（ ）
∴EG∥AD（ ）
∴∠E=________（ ）、
∠1=__________（ ）
又∵∠E=∠1（已知）
∴∠2=∠3（ ）
∴AD平分∠BAC （ ）
【答案】垂直的定义；同位角相等，两直线平行；∠3；两直线平行，同位角相等；∠2；两直线平行，内错角相等；等量代换；角平分线的定义．
【解析】
根据平行线的判定与性质进行解答即可．
解：∵AD⊥BC于D，EG⊥BC（已知）
∴∠ADC=∠EGC=90°（垂直的定义）
∴EG∥AD，（同位角相等，两直线平行）
∴∠E=∠3（两直线平行，同位角相等）
∠1=∠2，（两直线平行，内错角相等）
又∵∠E=∠1（已知）
∴∠2=∠3，（等量代换）
∴AD平分∠BAC．（角平分线的定义）
故答案为：垂直的定义；同位角相等，两直线平行；∠3；两直线平行，同位角相等；∠2；两直线平行，内错角相等；等量代换；角平分线的定义．
期末1卷素质教育评估卷系列答案科目：初中数学 来源： 题型：
【题目】如图，∠AOB内有一点P
（1）过点P画PC∥OB交OA于点C，画PD∥OA交OB于点D
（2）写出图中互补的角
（3）写出图中相等的角
（4）试说明图某一对相等．
查看答案和解析>>
科目：初中数学 来源： 题型：
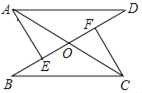
【题目】如图，已知AC、BD相交于点O，AD＝BC，AE⊥BD于点E，CF⊥BD于点F，BE＝DF．求证：
（1）△ADE≌△CBF；
（2）OA＝OC．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】联想三角形外心的概念，我们可引入如下概念。
定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心。
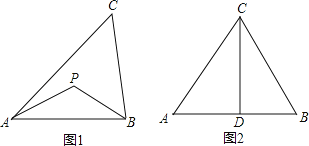
举例：如图1，若PA=PB，则点P为△ABC的准外心。
应用：如图2，CD为等边三角形ABC的高，准外心P在高CD上，且PD=
AB，求∠APB的度数。
探究：已知△ABC为直角三角形，斜边BC=5，AB=3，准外心P在AC边上，试探究PA的长。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE，则∠DEC的大小为 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的直角坐标系中，△ABC的顶点坐标分别是A(－4，－1)，B(1，1)，C(－1，4)；点
是△ABC内一点，当点平移到点
时．
①请写出平移后新
三个顶点的坐标；
②求的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
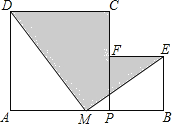
【题目】如图，点M是AB的中点，点P在MB上．分别以AP，PB为边，作正方形APCD和正方形PBEF，连结MD和ME．设AP＝a，BP＝b，且a+b＝10，ab＝20．则图中阴影部分的面积为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知ABCD的对角线AC，BD相交于点O，EF经过点O，分别交AD，BC于点E，F，且OE＝4，AB＝5，BC＝9，则四边形ABFE的周长是( )
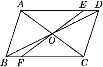
A. 13 B. 16 C. 22 D. 18
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知 AD⊥BC，垂足为点 D，EF⊥BC，垂足为点 F，∠1+∠2=180°， 请填写∠CGD=∠CAB 的理由．
解：因为 AD⊥BC，EF⊥BC（ ）
所以∠ADC=90°，∠EFD=90°（ ）
得∠ADC=∠EFD（ ）
所以 AD//EF（ ）
得∠2+∠3=180° （ ）
又因为∠1+∠2=180°（已知）
所以∠1=∠3（ ）
所以 DG//AB（ ）
所以∠CGD=∠CAB（ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com