
【题目】如图,AB∥CD.∠1=∠2,∠3=∠4,试说明 AD∥BE,请你将下面解答过程填写完整.

解:∵AB∥CD,
∴∠4= ( )
∵∠3=∠4
∴∠3= (等量代换)
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAE 即∠BAE= .
∴∠3= ( )
∴AD∥BE( ).
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,∠DAC+∠ACB=180°,EF//BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°,则∠FEC的度数是( )
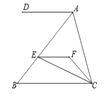
A.10°B.20°C.15°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划用![]() 元从厂家进
元从厂家进![]() 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,其中甲型
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,其中甲型![]() 元/台,每台获利
元/台,每台获利![]() 元;乙型
元;乙型![]() 元/台,每台获利
元/台,每台获利![]() 元;丙型
元;丙型![]() 元/台,每台获利
元/台,每台获利![]() 元.设甲、乙型设备应各买入
元.设甲、乙型设备应各买入![]() ,
,![]() 台:
台:
(1)购买丙型设备 台(用含![]() ,
,![]() 的代数式表示);
的代数式表示);
(2)若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了![]() 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?
(3)在第(2)题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形 BCDE 的各边分别平行于 x 轴或 y 轴,物体甲和物体乙分别由点 A(2,0)同时出发,沿长方形 BCDE 的边作环绕运动,物体甲按逆时针方向以 1 个单位/秒匀速运动,物体乙按顺时针方向以 2 个单位/秒匀速运动,则两个物体运动后的第 2020 次相遇地点的坐标是_____.
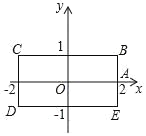
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2﹣3(x>0),y= ![]() (x>0),y=﹣
(x>0),y=﹣ ![]() (x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.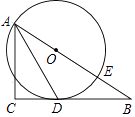
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将方格纸中的△ABC向上平移4个单位长度,然后向右平移6个单位长度,得到△A1B1C1.
(1)画出平移后的图形;
(2)线段AA1,BB1的位置关系是______;数量关系是________.
(3)如果每个方格的边长是1,那么△ABC的面积是___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com