
【题目】如图,点P( ![]() +1,
+1, ![]() ﹣1)在双曲线y=
﹣1)在双曲线y= ![]() (x>0)上.
(x>0)上.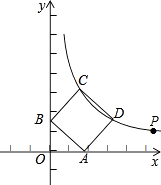
(1)求k的值;
(2)若正方形ABCD的顶点C,D在双曲线y= ![]() (x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
(x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
【答案】
(1)解:点P( ![]() ,
, ![]() )在双曲线
)在双曲线 ![]() 上,
上,
将x= ![]() ,y=
,y= ![]() 代入解析式可得:
代入解析式可得:
k=2;
(2)解:过点D作DE⊥OA于点E,过点C作CF⊥OB于点F, 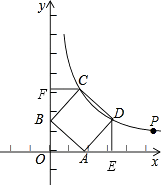
∵四边形ABCD是正方形,
∴AB=AD=BC,∠CBA=90°,
∴∠FBC+∠OBA=90°,
∵∠CFB=∠BOA=90°,
∴∠FCB+∠FBC=90°,
∴∠FBC=∠OAB,
在△CFB和△AOB中,
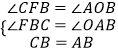 ,
,
∴△CFB≌△AOB(AAS),
同理可得:△BOA≌△AED≌△CFB,
∴CF=OB=AE=b,BF=OA=DE=a,
设A(a,0),B(0,b),
则D(a+b,a)C(b,a+b),
可得:b(a+b)=2,a(a+b)=2,
解得:a=b=1.
所以点C的坐标为:(1,2).
【解析】(1)由待定系数法把P坐标代入解析式即可;(2)C、D均在双曲线上,它们的坐标就适合解析式,设出C坐标,再由正方形的性质可得△CFB≌△AOB△BOA≌△AED≌△CFB,代入解析式得b(a+b)=2,a(a+b)=2,即可求出C坐标.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,若四边形ABCD为“可分四边形”,∠DAB为“可分角”,且∠DCB=∠DAB,则∠DAB=°.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
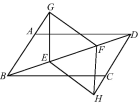
【题目】如图,在ABCD中,E,F是对角线BD上的两点,BE=DF,点G,H分别在BA和DC的延长线上,且AG=CH,连接GE,EH,HF,FG.
(1)求证:四边形GEHF是平行四边形;
(2)若点G,H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为t s,当t=时,△CPQ与△CBA相似.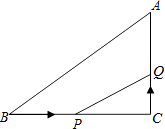
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).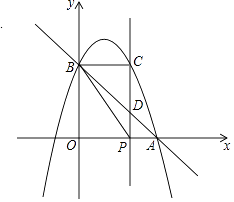
(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为 . (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100个,付款总额不得超过11815元.已知:厂家两种球的批发价如(表![]() )、商场在某两天的零售信息如(表
)、商场在某两天的零售信息如(表![]() ):
):
品名 | 厂家批发价(元/个) |
篮球 | 130 |
排球 | 100 |
(表![]() )
)
篮球(个) | 排球(个) | 零售总价(元) | |
第一天 | 8 | 5 | 1880 |
第二天 | 6 | 10 | 2160 |
(表![]() )
)
请解决以下问题:
(1)求出体育商场出售篮球和排球的零售单价.
(2)该采购员最多可从厂家购进篮球多少个.
(3)若该商场把这100个球全部以零售价售出,为使商场的利润不低于2580元,则采购员采购的方案有哪几种?该商场最多可盈利__________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:a*b=![]() ,则下列等式中对于任意实数 a、b、c 都成立的是( )
,则下列等式中对于任意实数 a、b、c 都成立的是( )
①a+(b*c)=(a+b)*(a+c) ②a*(b+c)=(a+b)*c
③a*(b+c)=(a*b)+(a*c) ④(a*b)+c= ![]() +(b*2c)
+(b*2c)
A. ①②③ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
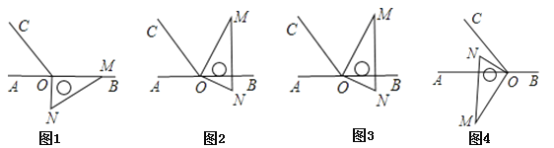
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)求∠CON的度数;
(2)如图2是将图1中的三角板绕点O按每秒15°的速度沿逆时针方向旋转一周的情况,在旋转的过程中,第t秒时,三条射线OA、OC、OM构成两个相等的角,求此时的t值
(3)将图1中的三角板绕点O顺时针旋转至图3(使ON在∠AOC的外部),图4(使ON在∠AOC的内部)请分别探究∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com