
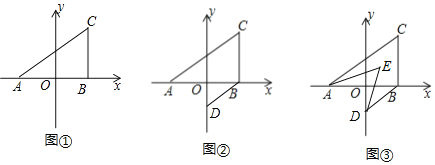
【题目】如图①,在平面直角坐标系中,点A、B在x轴上,AB⊥BC,AO=OB=2,BC=3
(1)写出点A、B、C的坐标.
(2)如图②,过点B作BD∥AC交y轴于点D,求∠CAB+∠BDO的大小.
(3)如图③,在图②中,作AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.
【答案】(1)A(﹣2,0),B(2,0),C(2,3);(2)90°;(3)45°.
【解析】
(1)根据图形和已知条件即可直接写出答案;
(2)根据两直线平行,内错角相等可得∠ABD=∠CAB,则∠CAB+∠BDO=∠ABD+∠BDO=90°;
(3)根据角平分线的定义可得∠CAE+∠BDE,过点E作EF∥AC,然后根据平行线的性质求出∠AED=∠CAE+∠BDE.
解:(1)在平面直角坐标系中,点A、B在x轴上,AO=OB=2,
∴A(﹣2,0),B(2,0),
∵AB⊥BC, BC=3,
∴C(2,3);
(2)在直角坐标系中,DO⊥AB,
∴∠ABD+∠BDO=90°,
∵BD∥AC,
∴∠ABD=∠CAB,
∴∠CAB+∠BDO =∠ABD+∠BDO=90°;
(3)由(2)得:∠CAB+∠BDO =90°,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠CAE=![]() ∠BAC ,∠BDE =
∠BAC ,∠BDE =![]() ∠BDO
∠BDO
∴∠CAE+∠BDE=![]() ∠BAC+
∠BAC+![]() ∠BDO=
∠BDO=![]() (∠BAC+∠BDO)=
(∠BAC+∠BDO)= ![]() ×90°=45°,
×90°=45°,
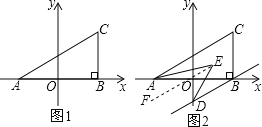
如图2,过点E作EF∥AC,
∴∠CAE=∠AEF,
又∵BD∥AC,
∴BD∥EF,
∴∠BDE=∠DEF,
∴∠AED=∠AEF+∠DEF=∠CAE+∠BDE=45°.


科目:初中数学 来源: 题型:
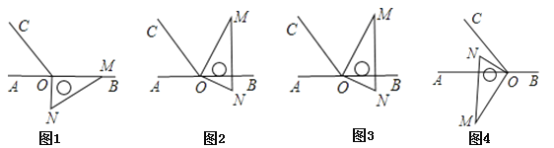
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)求∠CON的度数;
(2)如图2是将图1中的三角板绕点O按每秒15°的速度沿逆时针方向旋转一周的情况,在旋转的过程中,第t秒时,三条射线OA、OC、OM构成两个相等的角,求此时的t值
(3)将图1中的三角板绕点O顺时针旋转至图3(使ON在∠AOC的外部),图4(使ON在∠AOC的内部)请分别探究∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;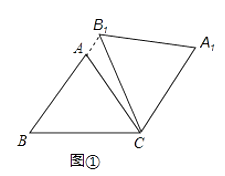
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.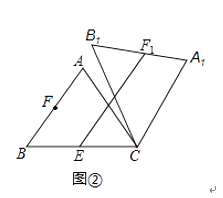
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
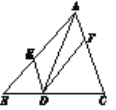
【题目】如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA.则下列说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形.
其中正确的是______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是 . 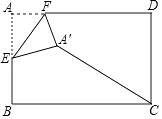
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com