
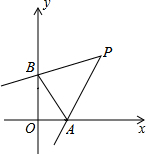
 如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是
如图,在直角坐标系中,点P(2,2),∠P=45°,∠P的两边分别交坐标轴于A、B两点,则三角形OAB的周长是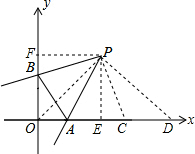 解:连接OP,作PF⊥y轴,PE⊥x轴,在x轴上截取ED=OF=OE=2,再截取DC=OB.
解:连接OP,作PF⊥y轴,PE⊥x轴,在x轴上截取ED=OF=OE=2,再截取DC=OB.
|
|
|


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| A、“13位同学中有两人出生的月份相同”是随机事件 |
| B、小亮掷硬币100次,其中44次正面朝上,则小亮掷硬币一次正面朝上的概率为0.44 |
| C、“明天降雨的概率是80%”,即明天下雨有80%的可能性 |
| D、彩票的中奖概率为1%,买100张才会中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:
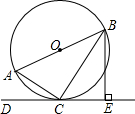 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线DC⊥BE于点E,BC平分∠ABE,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E,交BC于F.
如图,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E,交BC于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com