练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

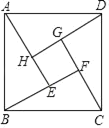
    【题目】如图所示图案是我国汉代数学家赵爽在注解《周髀算经》时给出的，人们称它为”赵爽弦图“．已知AE＝4，BE＝3，若向正方形ABCD内随意投掷飞镖（每次均落在正方形ABCD内，且落在正方形ABCD内任何一点的机会均等），则恰好落在正方形EFGH内的概率为（　　）

    A.B.C.D.

    【答案】A

    【解析】

    由AE=4，BE=3，得AB=5，所以正方形ABCD的面积：5×5=25，正方形EFGH的面积：25-4××3×4=1，则恰好落在正方形EFGH内的概率为．

    解：∵AE＝4，BE＝3，∠AEB=90°，

    ∴AB＝5，

    ∴正方形ABCD的面积：5×5＝25，

    正方形EFGH的面积：25﹣4×＝1，

    ∴恰好落在正方形EFGH内的概率为，

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】[提出问题]正多边形内任意一点到各边距离之和与这个正多边形的边及内角有什么关系？

    [探索发现]

    为了解决这个问题，我们不妨从最简单的正多边形-------正三角形入手

    如图①，是正三角形，边长是是内任意一点，到各边距离分别为，确定的值与的边及内角的关系．

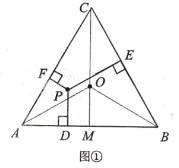
    如图②，五边形是正五边形，边长是是正五边形内任意一点，到五边形各边距离分别为， 参照的探索过程，确定的值与正五边形的边及内角的关系．

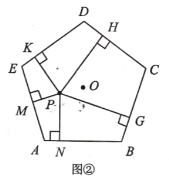
    类比上述探索过程：

    正六边形(边长为)内任意一点 到各边距离之和

    正八边形(边长为)内任意一点到各边距离之和

    [问题解决]正边形(边长为)内任意-一点P到各边距离之和

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，圆内接四边形ABCD，AD＝BC，AB是⊙O的直径．

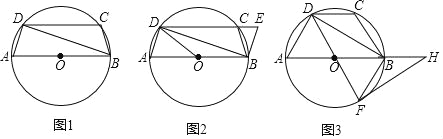
    （1）求证：AB∥CD；

    （2）如图2，连接OD，作∠CBE＝2∠ABD，BE交DC的延长线于点E，若AB＝6，AD＝2，求CE的长；

    （3）如图3，延长OB使得BH＝OB，DF是⊙O的直径，连接FH，若BD＝FH，求证：FH是⊙O的切线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线经过，两点，且与轴交于点，抛物线的对称轴是直线．

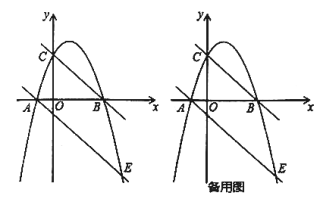
    （1）求抛物线的函数表达式；

    （2）抛物线与直线交于、两点，点在轴上且位于点的左侧，若以、、为顶点的三角形与相似，求点的坐标；

    （3）是直线上一动点，为抛物线上一动点，若为等腰直角三角形，请直接写出点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了解学生课外阅读情况，就学生每周阅读时间随机调查了部分学生，调查结果按性别整理如下：

    女生阅读时间人数统计表

    阅读时间（小时）

    人数

    占女生人数百分比

    4

    5

    6

    2

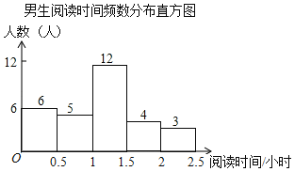
    根据图表解答下列问题：

    （1）在女生阅读时间人数统计表中，　 ，　 ；

    （2）此次抽样调查中，共抽取了　 名学生，学生阅读时间的中位数在　 时间段；

    （3）从阅读时间在2～2.5小时的5名学生中随机抽取2名学生参加市级阅读活动，恰好抽到男女生各一名的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在中，为延长线上一点，连接交的外接圆于点，连接

    （1）求证：平分；

    （2）若，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设二次函数y=（ax-1）（x-a），其中a是常数，且a≠0．

    （1）当a=2时，试判断点（-，-5）是否在该函数图象上．

    （2）若函数的图象经过点（1，-4），求该函数的表达式．

    （3）当-1≤x≤+1时，y随x的增大而减小，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

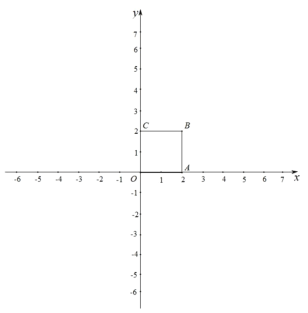
    【题目】对于平面内的点 P 和图形 M，给出如下定义：以点 P 为圆心，以 r 为半径作⊙P，使得图形 M 上的所有点都在⊙P 的内部（或边上），当 r 最小时，称⊙P 为图形 M 的 P 点 控制圆，此时，⊙P 的半径称为图形 M 的 P 点控制半径．已知，在平面直角坐标系中， 正方形 OABC 的位置如图所示，其中点 B（2，2）

    （1）已知点 D（1，0），正方形 OABC 的 D 点控制半径为 r1，正方形 OABC 的 A 点 控制半径为 r2，请比较大小：r1 r2；

    （2）连接 OB，点 F 是线段 OB 上的点，直线 l：y= x+b；若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点，求 b 的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形中，是边上的一动点（不与点、重合），连接，点关于直线的对称点为，连接并延长交于点，连接，过点作交的延长线于点，连接．

    （1）求证：；

    （2）用等式表示线段与的数量关系，并证明．

    查看答案和解析>>

    同步练习册答案