
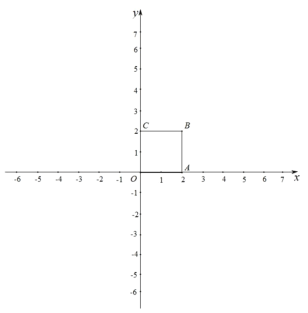
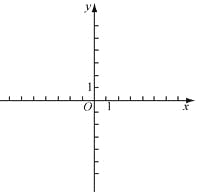
【题目】对于平面内的点 P 和图形 M,给出如下定义:以点 P 为圆心,以 r 为半径作⊙P,使得图形 M 上的所有点都在⊙P 的内部(或边上),当 r 最小时,称⊙P 为图形 M 的 P 点 控制圆,此时,⊙P 的半径称为图形 M 的 P 点控制半径.已知,在平面直角坐标系中, 正方形 OABC 的位置如图所示,其中点 B(2,2)
(1)已知点 D(1,0),正方形 OABC 的 D 点控制半径为 r1,正方形 OABC 的 A 点 控制半径为 r2,请比较大小:r1 r2;
(2)连接 OB,点 F 是线段 OB 上的点,直线 l:y= ![]() x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
【答案】(1)<;(2)![]() .
.
【解析】
(1)根据控制半径的定义求出r1和r2即可解决问题;
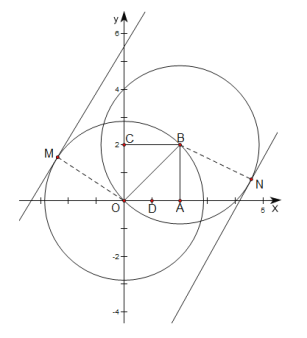
(2)如图所示,圆O和圆B分别是以O,B为圆心,以OB长为半径的圆,分别求出直线l与圆O相切,直线l与圆B相切时的b值,得到两种极限情况下的b值,即可得到b 的取值范围.
解:(1)由题意得:r1=BD=CD=![]() ,r2=AC=
,r2=AC=![]() ,
,
∴r1<r2;
(2)如图所示,圆O和圆B分别是以O,B为圆心,以OB长为半径的圆,
当直线l:![]() 与圆O相切于点M时,连接OM,可得OM与直线l垂直,
与圆O相切于点M时,连接OM,可得OM与直线l垂直,
则直线OM的解析式为:![]() ,
,
设M(x,![]() ),
),
∵OM=OB,
∴OM=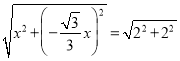 ,
,
∴![]() 或
或![]() (舍去),
(舍去),
∴M(![]() ,
,![]() ),
),
将(![]() ,
,![]() )代入
)代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
当直线l:![]() 与圆B相切于点N时,连接BN,
与圆B相切于点N时,连接BN,
同理可求出此时![]() ,
,
∴b的取值范围为:![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
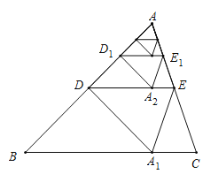
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() ,称为第
,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;还原纸片后,再将
;还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第
处,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;按上述方法不断操作下去…,经过第
;按上述方法不断操作下去…,经过第![]() 次操作后得到的折痕
次操作后得到的折痕![]() ,到
,到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,将点 A(2,4)向下平移 2 个单位得到点 C,反比例函数y ![]() (m≠0)的图象经过点 C,过点 C 作 CB⊥x 轴于点 B
(m≠0)的图象经过点 C,过点 C 作 CB⊥x 轴于点 B

(1)求 m 的值;
(2)一次函数 y=kx+b(k<0)的图象经过点 C,交 x 轴于点 D, 线段 CD,BD,BC 围成的区域(不含边界)为 G; 若横、纵坐标都是整数的点叫做整点
①b=3 时,直接写出区域 G 内的整点个数
②若区域 G 内没有整点,结合函数图象,确定 k 的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 在
在![]() 和
和![]() 时的函数值相等.
时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数![]() 的图象与二次函数的图象都经过点A
的图象与二次函数的图象都经过点A![]() ,求m和k的值;
,求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移![]() 个单位后得到的图象记为C,同时将(2)中得到的直线
个单位后得到的图象记为C,同时将(2)中得到的直线![]() 向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 内部做
内部做![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点:动点
的中点:动点![]() 由
由![]() 出发,沿
出发,沿![]() 运动,速度为每秒5个单位,动点
运动,速度为每秒5个单位,动点![]() 由
由![]() 出发,沿
出发,沿![]() 运动,速度为每秒8个单位,当点
运动,速度为每秒8个单位,当点![]() 到达点
到达点![]() 时,两点同时停止运动;过
时,两点同时停止运动;过![]() 、
、![]() 、
、![]() 作
作![]() ;
;
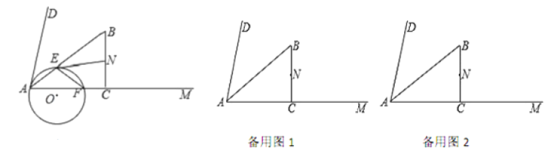
(1)判断![]() 的形状为________,并判断
的形状为________,并判断![]() 与
与![]() 的位置关系为__________;
的位置关系为__________;
(2)求![]() 为何值时,
为何值时,![]() 与
与![]() 相切?求出此时
相切?求出此时![]() 的半径,并比较半径与劣弧
的半径,并比较半径与劣弧![]() 长度的大小;
长度的大小;
(3)直接写出![]() 的内心运动的路径长为__________;(注:当
的内心运动的路径长为__________;(注:当![]() 、
、![]() 、
、![]() 重合时,内心就是
重合时,内心就是![]() 点)
点)
(4)直接写出线段![]() 与
与![]() 有两个公共点时,
有两个公共点时,![]() 的取值范围为__________.
的取值范围为__________.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
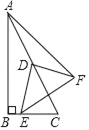
【题目】如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,点D是AC边的中点,E是直线BC上一动点,将线段DE绕点D逆时针旋转90°得到线段DF,连接AF、EF,在点E的运动过程中线段AF的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com