
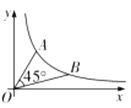
【题目】如图,点![]() 为反比例函数
为反比例函数![]() 图象上的两点,且满足
图象上的两点,且满足![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标是__________.
的坐标是__________.
【答案】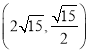
【解析】
如图,过A点作AO的垂线,交OB的延长线于C,过A点作y轴垂线AE,垂足为E,过C点作CD⊥AE于D,证明![]() ,得到
,得到![]() ,再求出直线OC解析式和反比例函数的解析式,联立方程组求解即可.
,再求出直线OC解析式和反比例函数的解析式,联立方程组求解即可.
如图,过A点作AO的垂线,交OB的延长线于C,过A点作y轴垂线AE,垂足为E,过C点作CD⊥AE于D,
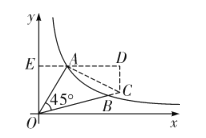
![]()
![]() ,
,
∴![]() ,
,
又![]() ,
,
∵∠CAD+∠OAE=90°,∠OAE+∠AOE=90°,
∴![]()
![]()
![]() ,
,
∴C点坐标为(8,2),A点坐标为(3,5)
设直线OC解析式为![]() ,
,
把C点坐标代入得,![]()
∴直线OC解析式为![]() ,
,
设反比例函数的解析式为![]() ,
,
把A点坐标代入得,k2=15,
∴反比例函数的解析式为![]() ,
,
联立方程组得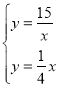 ,解得
,解得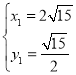 或
或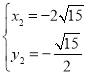
∵点B在第一象限,
∴B点坐标为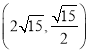 .
.


科目:初中数学 来源: 题型:
【题目】在一次购物中,小悦和小惠都准备从“微信”“支付宝”“银行卡”“现金”四种支付方式中任选一种进行支付.
(1)小悦用“微信”支付是__________事件(填“不可能”或“必然”或“随机”),小惠用“微信”支付的概率是__________.
(2)请用画树状图或列表的方法求出两人恰好选择同一种支付方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
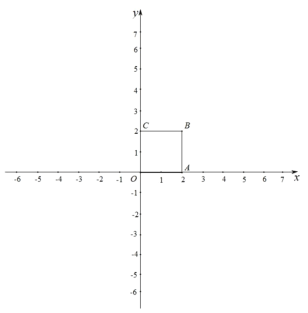
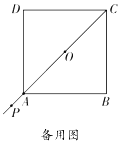
【题目】对于平面内的点 P 和图形 M,给出如下定义:以点 P 为圆心,以 r 为半径作⊙P,使得图形 M 上的所有点都在⊙P 的内部(或边上),当 r 最小时,称⊙P 为图形 M 的 P 点 控制圆,此时,⊙P 的半径称为图形 M 的 P 点控制半径.已知,在平面直角坐标系中, 正方形 OABC 的位置如图所示,其中点 B(2,2)
(1)已知点 D(1,0),正方形 OABC 的 D 点控制半径为 r1,正方形 OABC 的 A 点 控制半径为 r2,请比较大小:r1 r2;
(2)连接 OB,点 F 是线段 OB 上的点,直线 l:y= ![]() x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
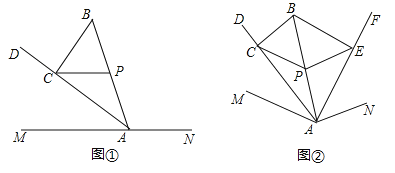
【题目】探究:如图①,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 外,连结
外,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
应用:如图②,点![]() 在
在![]() 内部,连结
内部,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ;作
;作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .若
.若![]() ,则
,则![]() 的大小为多少度.
的大小为多少度.
查看答案和解析>>
科目:初中数学 来源: 题型:
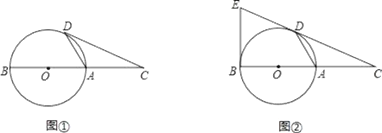
【题目】已知点C为直径BA的延长线上一点,CD切⊙O于点D,
(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知点![]() 为正方形
为正方形![]() 的对角线的交点,点
的对角线的交点,点![]() 是对角线
是对角线![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() 重合),分别过点
重合),分别过点![]() 向直线
向直线![]() 作垂线,垂足分别为点
作垂线,垂足分别为点![]() ,连接
,连接![]() 和
和![]() .
.
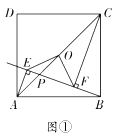

(1)求证:![]() ;
;
(2)如图②,延长正方形对角线![]() ,当点
,当点![]() 运动到
运动到![]() 的延长线上时,通过证明判断(1)中的结论是否仍然成立;
的延长线上时,通过证明判断(1)中的结论是否仍然成立;
(3)若点![]() 在射线
在射线![]() 上运动,
上运动,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
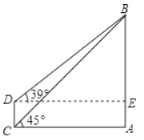
【题目】目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
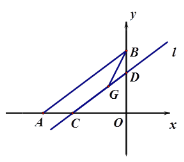
【题目】如图,已知A(-4,0)、B(0,3),一次函数![]() 与坐标轴分别交于C、D两点,G为CD上一点,且DG:CG=1:2,连接BG,当BG平分∠ABO时,则b的值为____.
与坐标轴分别交于C、D两点,G为CD上一点,且DG:CG=1:2,连接BG,当BG平分∠ABO时,则b的值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com