
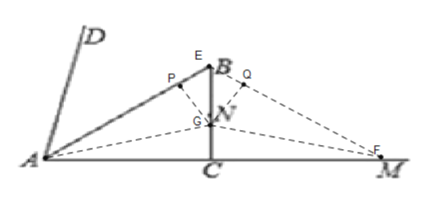
【题目】如图,在![]() 内部做
内部做![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点:动点
的中点:动点![]() 由
由![]() 出发,沿
出发,沿![]() 运动,速度为每秒5个单位,动点
运动,速度为每秒5个单位,动点![]() 由
由![]() 出发,沿
出发,沿![]() 运动,速度为每秒8个单位,当点
运动,速度为每秒8个单位,当点![]() 到达点
到达点![]() 时,两点同时停止运动;过
时,两点同时停止运动;过![]() 、
、![]() 、
、![]() 作
作![]() ;
;
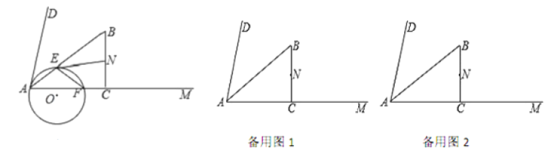
(1)判断![]() 的形状为________,并判断
的形状为________,并判断![]() 与
与![]() 的位置关系为__________;
的位置关系为__________;
(2)求![]() 为何值时,
为何值时,![]() 与
与![]() 相切?求出此时
相切?求出此时![]() 的半径,并比较半径与劣弧
的半径,并比较半径与劣弧![]() 长度的大小;
长度的大小;
(3)直接写出![]() 的内心运动的路径长为__________;(注:当
的内心运动的路径长为__________;(注:当![]() 、
、![]() 、
、![]() 重合时,内心就是
重合时,内心就是![]() 点)
点)
(4)直接写出线段![]() 与
与![]() 有两个公共点时,
有两个公共点时,![]() 的取值范围为__________.
的取值范围为__________.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)△AEF为等腰三角形;DA与![]() 相切;(2)劣弧
相切;(2)劣弧![]() 长度>半径;(3)
长度>半径;(3)![]() 的内心运动的路径长为
的内心运动的路径长为![]() ;(4)线段
;(4)线段![]() 与
与![]() 有两个公共点时,
有两个公共点时,![]() 的取值范围为
的取值范围为![]() .
.
【解析】
(1)过点E作EH⊥AF于点H,连接OH,OA,证明△AEH∽△ABC,得到AH=FH,即可证明为等腰三角形;根据圆周角和圆心角证明∠DAC=∠AOE,即可证明∠DAO=90°;
(2)连接EO,AO,OF,交AC于点H,根据相切知四边形EHCN为矩形,从而求出t,在Rt△AOH中,根据勾股定理求出半径,然后求出∠AOH的度数即可比较;
(3)得到![]() 的内心运动的路径长为AG,然后根据面积求出内切圆半径,从而求出AG长;
的内心运动的路径长为AG,然后根据面积求出内切圆半径,从而求出AG长;
(4)分别讨论两种极限位置,①当MN与![]() 相切时,②当N在圆上时,即ON为半径,分别求出t的值,即可确定t的取值范围.
相切时,②当N在圆上时,即ON为半径,分别求出t的值,即可确定t的取值范围.
解:(1)过点E作EH⊥AF于点H,连接OH,OA,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
设运动时间为t,
∴AE=5t,AF=8t,
∵EH⊥AF,
∴△AEH∽△ABC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴FH=4t,
∴AH=FH,
∴△AEF为等腰三角形;
∴E为![]() 的中点,
的中点,
∴H为AF的中点,
∴OH垂直AC,
∴∠OAF+∠AOE=90°,
∴∠AOE=2∠EFA,
∵AB平分∠DAC,∠EAC=∠EFA,
∴∠DAC=∠AOE,
∴∠DAC+∠AOE=90°,
∴∠DAO=90°,
∴DA与![]() 相切;
相切;
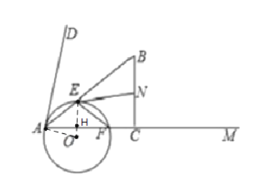
(2)连接EO,AO,OF,交AC于点H,
由(1)知EH⊥AC,
∵EN与![]() 相切,
相切,
∴∠OEN=90°,
∴四边形EHCN为矩形,
在Rt△AHE中,
![]() ,
,
∴NC=EH=3t,
∵N是BC中点,
∴BC=6t,
∵BC=6,
∴6t=6,
解得:t=1,
∴AH=4,EH=3,
设半径为x,
∴OH=x-3,
在Rt△AOH中,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴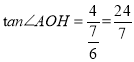 ,
,
∴∠AOH=74°,
∴∠AOH>60°,
∴AE>半径,
∴劣弧![]() 长度>半径;
长度>半径;
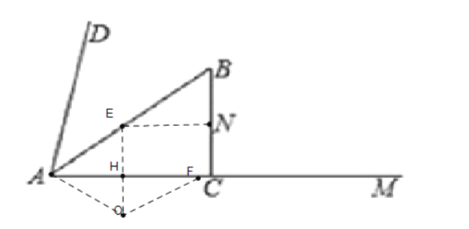
(3)当E运动到B点时,
t=10÷5=2,
∴AF=2×8=16,
此时△AEF的内心记为G,
当A、E、F三点重合时,内心为A,
∴![]() 的内心运动的路径长为AG,
的内心运动的路径长为AG,
作GP⊥AE于点P,GQ⊥EF于点Q,
S△AEF=![]() ,
,
设CG=a,
∴S△AEF=S△AGF+S△AEG+S△FEG,
∴![]() ,
,
解得:![]() ,
,
在Rt△ACG中,
![]() ,即
,即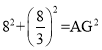 ,
,
∴AG=![]() ,
,
∴![]() 的内心运动的路径长为
的内心运动的路径长为![]() ;
;
(4)分别讨论两种极限位置,
①当MN与![]() 相切时,
相切时,
由(2)知,t=1;
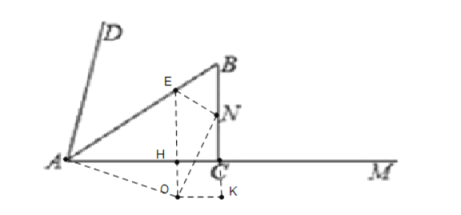
②当N在圆上时,即ON为半径,如图所示:
则OE=ON,
∴AH=4t,EH=3t,
设半径为x,
则在Rt△AOH中,![]()
![]() ,
,
解得:![]() ,
,
∴CK=OH=![]() ,
,
在Rt△OKN中,
![]() ,
,
∴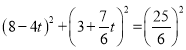 ,
,
解得:![]() ,
,
∴线段![]() 与
与![]() 有两个公共点时,
有两个公共点时,![]() 的取值范围为
的取值范围为![]() .
.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)如图1,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() ,若
,若![]() ,则
,则![]() ________.
________.
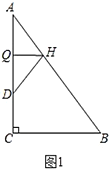
(2)如图2,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() .若
.若![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
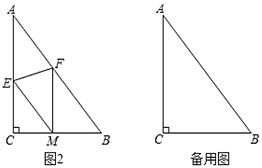
(3)在(1)(2)的条件下,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.
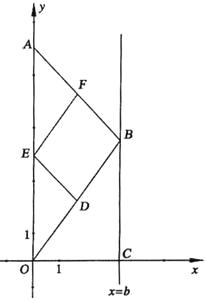
(1)判断四边形DEFB的形状.并证明你的结论;
(2)试求四边形DEFB的面积S与b的关系式;
(3)设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
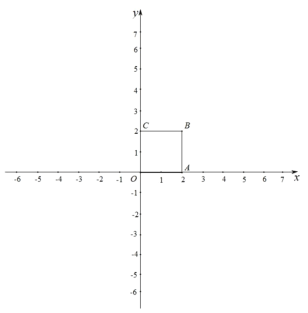
【题目】对于平面内的点 P 和图形 M,给出如下定义:以点 P 为圆心,以 r 为半径作⊙P,使得图形 M 上的所有点都在⊙P 的内部(或边上),当 r 最小时,称⊙P 为图形 M 的 P 点 控制圆,此时,⊙P 的半径称为图形 M 的 P 点控制半径.已知,在平面直角坐标系中, 正方形 OABC 的位置如图所示,其中点 B(2,2)
(1)已知点 D(1,0),正方形 OABC 的 D 点控制半径为 r1,正方形 OABC 的 A 点 控制半径为 r2,请比较大小:r1 r2;
(2)连接 OB,点 F 是线段 OB 上的点,直线 l:y= ![]() x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解密数学魔术:魔术师请观众心想一个数,然后将这个数按以下步骤操作:
![]()
魔术师能立刻说出观众想的那个数.
(1)如果小玲想的数是![]() ,请你通过计算帮助她告诉魔术师的结果;
,请你通过计算帮助她告诉魔术师的结果;
(2)如果小明想了一个数计算后,告诉魔术师结果为85,那么魔术师立刻说出小明想的那个数是:__________;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.若设观众心想的数为![]() ,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
查看答案和解析>>
科目:初中数学 来源: 题型:
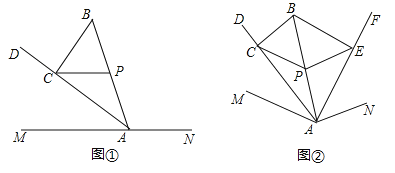
【题目】探究:如图①,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 外,连结
外,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
应用:如图②,点![]() 在
在![]() 内部,连结
内部,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ;作
;作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .若
.若![]() ,则
,则![]() 的大小为多少度.
的大小为多少度.
查看答案和解析>>
科目:初中数学 来源: 题型:
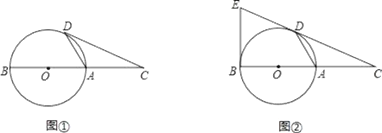
【题目】已知点C为直径BA的延长线上一点,CD切⊙O于点D,
(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(5,0)、C(0,﹣5)三点.
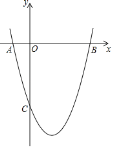
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<5时,y的取值范围为 ;
(3)点P为抛物线上一点,若S△PAB=21,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com