
【题目】已知二次函数![]() 在
在![]() 和
和![]() 时的函数值相等.
时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数![]() 的图象与二次函数的图象都经过点A
的图象与二次函数的图象都经过点A![]() ,求m和k的值;
,求m和k的值;
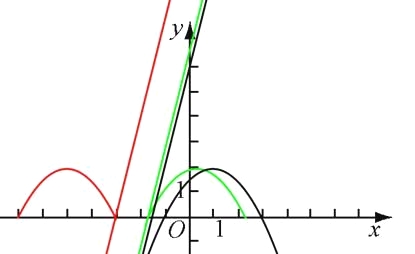
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移![]() 个单位后得到的图象记为C,同时将(2)中得到的直线
个单位后得到的图象记为C,同时将(2)中得到的直线![]() 向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
【答案】(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
【解析】
(1)由二次函数在![]() 和
和![]() 时的函数值相等,可知二次函数图象的对称轴为
时的函数值相等,可知二次函数图象的对称轴为![]() ,从而由对称轴公式
,从而由对称轴公式![]() ,可求得
,可求得![]() ,从而求得二次函数的解析式.
,从而求得二次函数的解析式.
(2)由二次函数图象经过A![]() 点代入
点代入![]() 可求得
可求得![]() ,从而由一次函数
,从而由一次函数![]() 的图象经过A点,代入可求得
的图象经过A点,代入可求得![]() .
.
(3)根据平移的性质,求得平移后的二次函数和一次函数表达式,根据平移后的直线与图象C有公共点,求得公共点的坐标即可.
解:(1)∵二次函数在![]() 和
和![]() 时的函数值相等,
时的函数值相等,
∴二次函数图象的对称轴为![]() .
.
∴![]() ,解得
,解得![]() .
.
∴二次函数解析式为![]() .
.
(2)∵二次函数图象经过A![]() 点,
点,
∴![]() ,A(-3,-6).
,A(-3,-6).
又∵一次函数![]() 的图象经过A点,
的图象经过A点,
∴![]() ,解得
,解得![]() .
.
(3)由题意可知,二次函数在点B,C间的部分图象的解析式为
![]() ,
,![]() ,
,
则向左平移后得到的图象C的解析式为![]() ,
,![]() .
.
此时一次函数![]() 的图象平移后的解析式为
的图象平移后的解析式为![]() .
.
∵平移后的直线与图象C有公共点,
∴两个临界的交点为![]() 与
与![]() .
.
∴当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() .
.
∴![]()


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
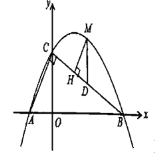
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在
在![]() 轴上,
轴上,![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)点![]() 是直线
是直线![]() 上方抛物线上的一点,过点
上方抛物线上的一点,过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 周长的最大值.
周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,G是边AB的中点,平行于AB的动直线l分别交△ABC的边CA、CB于点M、N,设CM=m.
(1)当m=1时,求△MNG的面积;
(2)若点G关于直线l的对称点为点G′,请求出点G′ 恰好落在△ABC的内部(不含边界)时,m的取值范围;
(3)△MNG是否可能为直角三角形?如果能,请求出所有符合条件的m的值;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
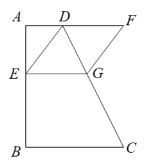
【题目】四边形 ABCD 中,∠A=∠B= 90°,点 E 在边 AB 上,点 F 在 AD 的延长线上,且 点 E 与点 F 关于直线 CD 对称,过点 E 作 EG∥AF 交 CD 于点 G,连接 FG,DE.
(1)求证:四边形 DEGF 是菱形;
(2)若 AB=10,AF=BC=8,求四边形 DEGF 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
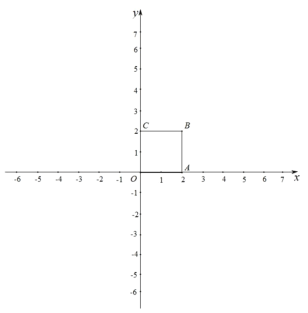
【题目】对于平面内的点 P 和图形 M,给出如下定义:以点 P 为圆心,以 r 为半径作⊙P,使得图形 M 上的所有点都在⊙P 的内部(或边上),当 r 最小时,称⊙P 为图形 M 的 P 点 控制圆,此时,⊙P 的半径称为图形 M 的 P 点控制半径.已知,在平面直角坐标系中, 正方形 OABC 的位置如图所示,其中点 B(2,2)
(1)已知点 D(1,0),正方形 OABC 的 D 点控制半径为 r1,正方形 OABC 的 A 点 控制半径为 r2,请比较大小:r1 r2;
(2)连接 OB,点 F 是线段 OB 上的点,直线 l:y= ![]() x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲乙两个玩具小汽车在笔直的240米跑道![]() 上进行折返跑游戏,甲从点
上进行折返跑游戏,甲从点![]() 出发,匀速在
出发,匀速在![]() 、
、![]() 之间折返跑,同时乙从点
之间折返跑,同时乙从点![]() 出发,以大于甲的速度匀速在
出发,以大于甲的速度匀速在![]() 、
、![]() 之间折返跑.在折返点的时间忽略不计.
之间折返跑.在折返点的时间忽略不计.

(1)若甲的速度为![]() ,乙的速度为
,乙的速度为![]() ,第一次迎面相遇的时间为
,第一次迎面相遇的时间为![]() ,则
,则![]() 与
与![]() 的关系式___________;
的关系式___________;
(注释:当两车相向而行时相遇是迎面相遇,当两车在![]() 点相遇时也视为迎面相遇)
点相遇时也视为迎面相遇)
(2)如图1,
①若甲乙两车在距![]() 点20米处第一次迎面相遇,则他们在距
点20米处第一次迎面相遇,则他们在距![]() 点_______米第二次迎面相遇:
点_______米第二次迎面相遇:
②若甲乙两车在距![]() 点50米处第一次迎面相遇,则他们在距
点50米处第一次迎面相遇,则他们在距![]() 点__________米第二次迎面相遇;
点__________米第二次迎面相遇;
(3)设甲乙两车在距![]() 点
点![]() 米处第一次迎面相遇,在距
米处第一次迎面相遇,在距![]() 点
点![]() 米处第二次迎面相遇.某同学发现了
米处第二次迎面相遇.某同学发现了![]() 与
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图2所示).
,如图2所示).
①则![]() _______,并在图2中补全
_______,并在图2中补全![]() 与
与![]() 的函数图象(在图中注明关键点的数据);
的函数图象(在图中注明关键点的数据);
②分别求出各部分图象对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 外,连结
外,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
应用:如图②,点![]() 在
在![]() 内部,连结
内部,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ;作
;作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .若
.若![]() ,则
,则![]() 的大小为多少度.
的大小为多少度.
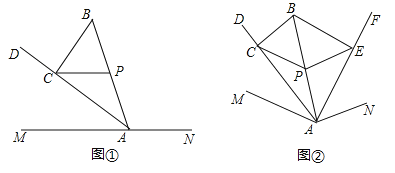
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知点![]() 为正方形
为正方形![]() 的对角线的交点,点
的对角线的交点,点![]() 是对角线
是对角线![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() 重合),分别过点
重合),分别过点![]() 向直线
向直线![]() 作垂线,垂足分别为点
作垂线,垂足分别为点![]() ,连接
,连接![]() 和
和![]() .
.
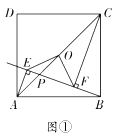

(1)求证:![]() ;
;
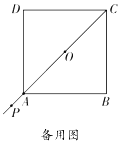
(2)如图②,延长正方形对角线![]() ,当点
,当点![]() 运动到
运动到![]() 的延长线上时,通过证明判断(1)中的结论是否仍然成立;
的延长线上时,通过证明判断(1)中的结论是否仍然成立;
(3)若点![]() 在射线
在射线![]() 上运动,
上运动,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合与实践﹣﹣探究图形中角之间的等量关系及相关问题.
问题情境:
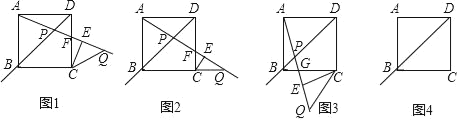
正方形ABCD中,点P是射线DB上的一个动点,过点C作CE⊥AP于点E,点Q与点P关于点E对称,连接CQ,设∠DAP=α(0°<α<135°),∠QCE=β.
初步探究:
(1)如图1,为探究α与β的关系,勤思小组的同学画出了0°<α<45°时的情形,射线AP与边CD交于点F.他们得出此时α与β的关系是β=2α.借助这一结论可得当点Q恰好落在线段BC的延长线上(如图2)时,α= °,β= °;
深入探究:
(2)敏学小组的同学画出45°<α<90°时的图形如图3,射线AP与边BC交于点G.请猜想此时α与β之间的等量关系,并证明结论;
拓展延伸:
(3)请你借助图4进一步探究:①当90°<α<135°时,α与β之间的等量关系为 ;
②已知正方形边长为2,在点P运动过程中,当α=β时,PQ的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com