
【题目】合与实践﹣﹣探究图形中角之间的等量关系及相关问题.
问题情境:
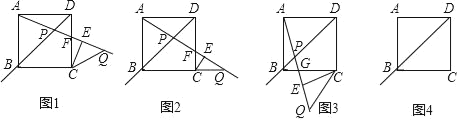
正方形ABCD中,点P是射线DB上的一个动点,过点C作CE⊥AP于点E,点Q与点P关于点E对称,连接CQ,设∠DAP=α(0°<α<135°),∠QCE=β.
初步探究:
(1)如图1,为探究α与β的关系,勤思小组的同学画出了0°<α<45°时的情形,射线AP与边CD交于点F.他们得出此时α与β的关系是β=2α.借助这一结论可得当点Q恰好落在线段BC的延长线上(如图2)时,α= °,β= °;
深入探究:
(2)敏学小组的同学画出45°<α<90°时的图形如图3,射线AP与边BC交于点G.请猜想此时α与β之间的等量关系,并证明结论;
拓展延伸:
(3)请你借助图4进一步探究:①当90°<α<135°时,α与β之间的等量关系为 ;
②已知正方形边长为2,在点P运动过程中,当α=β时,PQ的长为 .
【答案】(1)30,60;(2)α与β的关系是β=2(90°﹣α);理由见解析;(3)①β=2(α﹣90°);②6﹣2![]() .
.
【解析】
初步探究:(1)连接PC,由对称的性质和等腰三角形的性质得出∠QCE=∠PCE,证明△ABP≌△CBP,得出∠BAP=∠BCP,由平行线得出∠CQE=∠DAP=α,证出α+β=90°①,再证出β=2α②,即可得出结果;
深入探究:(2)连接PC,由对称的性质和等腰三角形的性质得出∠QCE=∠PCE,证明△ABP≌△CBP,得出∠BAP=∠BCP=∠BAD-∠DAP=90°-α,AP=CP,证出∠BAP=∠GCE,得出∠BCG=∠GCE=90°-α,即可得出结论;
拓展延伸:(3)①连接PC,证出∠PCE=∠QCE=β,证明△ABP≌△CBP,得出∠BAP=∠BCP=∠DAP-∠BAD=α-90°,证明∠BAP=∠BCH,得出∠BCP=∠BCH=∠BAP=α-90°,即可得出结论;
②分三种情况:
当0°<α<45°时,β=2α,不合题意;
当45°<α<90°时,β=2(90°-α),得出α=β=60°,作PM⊥AD于M,证出AM=![]() AP,DM=PM=
AP,DM=PM=![]() AM,设AM=x,则CP=AP=2x,DM=PM=
AM,设AM=x,则CP=AP=2x,DM=PM=![]() x,得出方程,解得:x=
x,得出方程,解得:x=![]() ,得出CP=AP=2x=2
,得出CP=AP=2x=2![]() -2,在△PCQ中,求出CE=
-2,在△PCQ中,求出CE=![]() CP=
CP=![]() -1,PE=
-1,PE=![]() CE=3-
CE=3-![]() ,得出PQ=2PE=6-2
,得出PQ=2PE=6-2![]() ;
;
当90°<α<135°时,β=2(α-90°),得出α=β=180°,不合题意.
解:(1)连接PC,如图2所示:
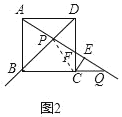
∵点Q与点P关于点E对称,
∴EP=EQ,
∵CE⊥AP,
∴CE垂直平分PQ,
∴CP=CQ,
∴∠QCE=∠PCE,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=90°,AD∥BC,∠ABD=∠CBD=45°,
在△ABP和△CBP中,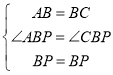 ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP,
∵AD∥BC,
∴∠CQE=∠DAP=α,
∵CE⊥AP,
∴∠CQE+∠QCE=90°,即α+β=90°①,
∵∠CQE+∠BAP=90°,
∴∠QCE=∠BAP=∠BCP,
∵∠BCP=∠CQE+∠CPQ,
∴β=2α②,
由①②得:α=30°,β=60°;
故答案为:30,60;
深入探究:
(2)α与β的关系是β=2(90°﹣α);理由如下:
连接PC,如图3所示:

∵点Q与点P关于点E对称,
∴EP=EQ,
∵CE⊥AP,
∴CE垂直平分PQ,
∴CP=CQ,
∴∠QCE=∠PCE,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=90°,∠ABD=∠CBD=45°,
在△ABP和△CBP中, ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=∠BAD﹣∠DAP=90°﹣α,AP=CP,
∵∠ABG=∠CEG=90°,
∴∠BAP+∠AGB=90°,∠GCE+∠CGE=90°,
∵∠AGB=∠CGE,
∴∠BAP=∠GCE,
∴∠BCG=∠GCE=90°﹣α,
∴∠QCE=2∠GCE=2(90°﹣α),
即:β=2(90°﹣α);
拓展延伸:
(3)①当90°<α<135°时,α与β之间的等量关系为β=2(α﹣90°);理由如下:
连接PC,设CE交AB于点H,如图4所示:
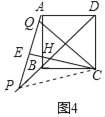
∵点Q与点P关于点E对称,
∴EP=EQ,
∵CE⊥AP,
∴CE垂直平分PQ,
∴CP=CQ,
∴∠PCE=∠QCE=β,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=90°,∠ABD=∠CBD=45°,
∴∠ABP=∠CBP,
在△ABP和△CBP中, ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=∠DAP﹣∠BAD=α﹣90°,
∵∠AEH=∠CBH=90°,
∴∠BAP+∠AHE=90°,∠BCH+∠BHC=90°,
∵∠AHE=∠CHB,
∴∠BAP=∠BCH,
∴∠BCP=∠BCH=∠BAP=α﹣90°,
∴∠QCE=∠PCE=2∠BCP=2(α﹣90°),
即:β=2(α﹣90°);
故答案为:β=2(α﹣90°);
②当0°<α<45°时,β=2α,不合题意;
当45°<α<90°时,β=2(90°﹣α),
∵α=β,
∴α=β=60°,
作PM⊥AD于M,如图5所示:
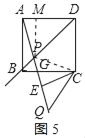
∵∠APM=90°﹣α=30°,∠PDM=45°,
∴AM=![]() AP,DM=PM=
AP,DM=PM=![]() AM,
AM,
设AM=x,则CP=AP=2x,DM=PM=![]() x,
x,
∵AD=2,
∴x+![]() x=2,
x=2,
解得:x=![]() ﹣1,
﹣1,
∴CP=AP=2x=2﹣![]() ,
,
∵∠PCQ=2β=120°,CP=CQ,CE⊥AP,
∴∠CPE=30°,PE=QE,
∴CE=![]() CP=
CP=![]() ﹣1,PE=
﹣1,PE=![]() CE=3﹣
CE=3﹣![]() ,
,
∴PQ=2PE=6﹣2![]() ;
;
当90°<α<135°时,β=2(α﹣90°),
∵α=β,
∴α=β=180°,不合题意;
综上所述,在点P运动过程中,当α=β时,PQ的长为6﹣2![]() ;
;
故答案为:6﹣2![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 在
在![]() 和
和![]() 时的函数值相等.
时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数![]() 的图象与二次函数的图象都经过点A
的图象与二次函数的图象都经过点A![]() ,求m和k的值;
,求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移![]() 个单位后得到的图象记为C,同时将(2)中得到的直线
个单位后得到的图象记为C,同时将(2)中得到的直线![]() 向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
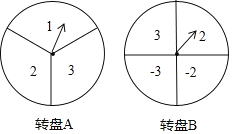
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李叔叔和张阿姨栽树.李叔叔栽6棵树所用的时间与张阿姨栽5棵树所用的时间相同,已知李叔叔比张阿姨平均每天多栽20棵树.
(1)求李叔叔平均每天栽树的棵数;
(2)由李叔叔和张阿姨同时栽树1540棵,要几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,点D是AC边的中点,E是直线BC上一动点,将线段DE绕点D逆时针旋转90°得到线段DF,连接AF、EF,在点E的运动过程中线段AF的最小值为_____.
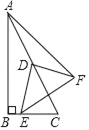
查看答案和解析>>
科目:初中数学 来源: 题型:
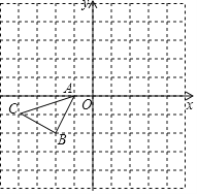
【题目】如图,方格纸中的每个小正方形的边长都为1,在建立平面直角坐标系后,△ABC的顶点均在格点上.
(1)以点A为旋转中心,将△ABC绕点A顺时针旋转90°得到△AB1C1,画出△AB1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2,若点B的坐标为(-2,-2),则点B2的坐标为_________.
(3)若△A2B2C2可看作是由△AB1C1绕点P顺时针旋转90°得到的,则点P的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼”便是其中一题.下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八.问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的![]() ,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
A.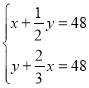 B.
B.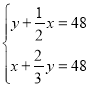 C.
C.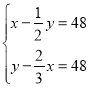 D.
D.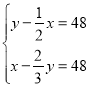
查看答案和解析>>
科目:初中数学 来源: 题型:
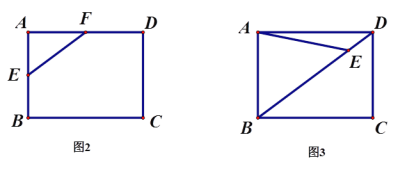
【题目】按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,矩形ABCD的顶点A、D在圆上, B、C两点在圆内,已知圆心O,请仅用无刻度的直尺作图,请作出直线l⊥AD;
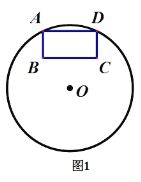
(2)请仅用无刻度的直尺在下列图2和图3中按要求作图.(补上所作图形顶点字母)
①图2是矩形ABCD,E,F分别是AB和AD的中点,以EF为边作一个菱形;
②图3是矩形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边作一个平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
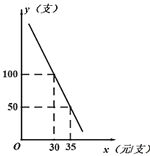
【题目】某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)请求出y与x的函数关系式;
(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)近期武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出 200 元捐赠给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定该款电动牙刷的售单价?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com