练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

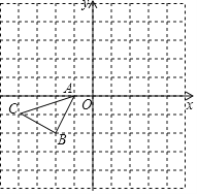
    【题目】如图，方格纸中的每个小正方形的边长都为1，在建立平面直角坐标系后，△ABC的顶点均在格点上．

    （1）以点A为旋转中心，将△ABC绕点A顺时针旋转90°得到△AB1C1，画出△AB1C1；

    （2）画出△ABC关于原点O成中心对称的△A2B2C2，若点B的坐标为（-2，-2），则点B2的坐标为_________．

    （3）若△A2B2C2可看作是由△AB1C1绕点P顺时针旋转90°得到的，则点P的坐标为______.

    【答案】（1）见解析；（2）图见解析；（2，2）；（3）（0，-1）

    【解析】

    （1）利用网格特点和旋转的性质画出B、C的对应点B1、C1，从而得到△AB1C1．

    （2）利用关于原点对称的点的坐标特征写出A2、B2、C2的坐标，然后描点连线即可；

    （3）连接A1A2，C1C2，作A1A2和C1C2的垂直平分线交于点P，观察图形即可得出结论．

    （1）如图，△AB1C1为所作；

    （2）如图，△A2B2C2为所作；若点B的坐标为（-2，-2），则点B2的坐标为（2，2）；

    （3）连接A1A2，C1C2，作A1A2和C1C2的垂直平分线交于点P，由图可知：P（0，-1）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，矩形OABC的对角线AC=12，∠ACO=30°

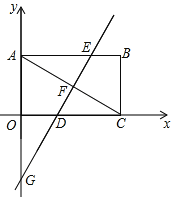
    （1）求B、C两点的坐标；

    （2）过点G（）作GF⊥AC，垂足为F，直线GF分别交AB、OC于点E、D，求直线DE的解析式；

    （3）在⑵的条件下，若点M在直线DE上，平面内是否存在点P，使以O、F、M、P为顶点的四边形是菱形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分如图，在ABCD中，点E、F分别是AD、BC的中点，分别连接BE、DF、BD．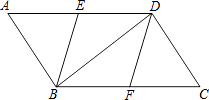

    （1）求证：△AEB≌△CFD；
    （2）若四边形EBFD是菱形，求∠ABD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．

    （1）写出你所学过的特殊四边形中是勾股四边形的两种图形的名称　　　　　　，　　　　　　；

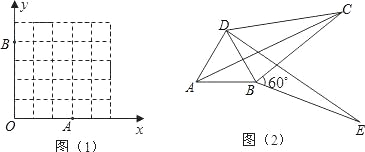
    （2）如图1，已知格点（小正方形的顶点）O（0，0），A（3，0），B（0，4），请你直接写出所有以格点为顶点，OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标．

    （3）如图2，将△ABC绕顶点B按顺时针方向旋转60°，得到△DBE，连接AD、DC，∠DCB=30°．求证：DC2+BC2=AC2，即四边形ABCD是勾股四边形．

    （4）若将图2中△ABC绕顶点B按顺时针方向旋转a度（0°＜a＜90°），得到△DBE，连接AD、DC，则∠DCB=　　　　　　°，四边形ABCD是勾股四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，线段AB在x轴上点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．得平行四边形ABDC

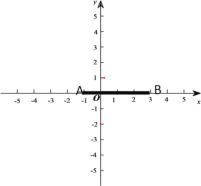
    （1）补全图形，直接写出点C，D的坐标；

    （2）若在y轴上存在点M，连接MA，MB，使S△MAB=S四边形ABDC，求出点M的坐标．

    （3）若点P在直线BD上运动，连接PC，PO．请画出图形，探索∠CPO、∠DCP、∠BOP的数量关系并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查，根据男生1000米及女生800米测试成绩整理，绘制成不完整的统计图，（图①，图②），请根据统计图提供的信息，回答下列问题：

    （1）该校毕业生中男生有 人；扇形统计图中a= ；

    （2）补全条形统计图；

    （3）若500名学生中随机抽取一名学生，这名学生该项成绩在8分及8分以下的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠MON = 50°，OE 平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合)，连接AC交射线OE于点D、设∠OAC = x°．


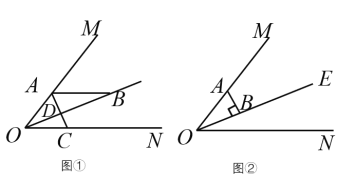
    （1）如图①，若AB//ON，

    ①则∠ABO 的度数是________；

    ②当∠BAD =∠ABD 时，x=_______；当∠BAD = ∠BDA 时，x=________．

    （2）如图②，若AB⊥OE，则是否存在这样的x值，使得 △ABD 中有一个角是另一个角的两倍．存在，直接写出x的值；不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，将边BC沿斜边上的中线CD折叠到CB′，若∠B=48°，则∠ACB′= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数y= 的图象经过点M（2，1）
    （1）求该函数的表达式；
    （2）当2＜x＜4时，求y的取值范围（直接写出结果）．

    查看答案和解析>>

    同步练习册答案