
【题目】如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=48°,则∠ACB′= . 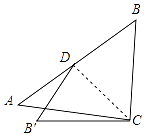
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A. OA=OC,OB=ODB. OA=OC,AB∥CD
C. AB=CD,OA=OCD. ∠ADB=∠CBD,∠BAD=∠BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
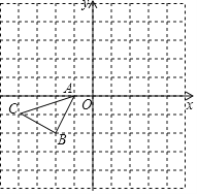
【题目】如图,方格纸中的每个小正方形的边长都为1,在建立平面直角坐标系后,△ABC的顶点均在格点上.
(1)以点A为旋转中心,将△ABC绕点A顺时针旋转90°得到△AB1C1,画出△AB1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2,若点B的坐标为(-2,-2),则点B2的坐标为_________.
(3)若△A2B2C2可看作是由△AB1C1绕点P顺时针旋转90°得到的,则点P的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=![]() (AC﹣AB);
(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF之间的数量关系。

查看答案和解析>>
科目:初中数学 来源: 题型:
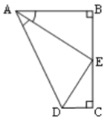
【题目】如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1, ![]() ).
).
(1)求tan∠OPQ的值;
(2)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,CA=CB,在△AED中,DA=DE,点D,E分别在CA,AB上.
(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是;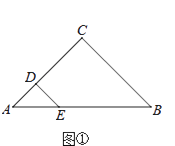
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是;,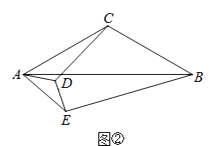
(3)若∠ACB=∠ADE=2α(0°<α<90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).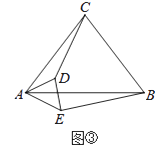
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小满的一次作业,老师说小满的解题过程不完全正确,并在作业旁写出了批改.
长跑比赛中,张华跑在前面,在离终点![]() 时他以
时他以![]() 的速度向终点冲刺,在他身后
的速度向终点冲刺,在他身后![]() 的李明需以多快的速度同时开始冲刺,才能在张华之前到达终点?
的李明需以多快的速度同时开始冲刺,才能在张华之前到达终点?
解:设李明以![]() 的速度开始冲刺,
的速度开始冲刺,
依题意,得![]() ,
,

两边同时除以25,得![]() .
.
答:李明需以大于![]() 的速度同时开始冲刺,才能在张华之前到达终点.
的速度同时开始冲刺,才能在张华之前到达终点.
请回答:必须添加“根据实际意义可知,![]() ”这个条件的理由是_______________________.
”这个条件的理由是_______________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com