
【题目】已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1, ![]() ).
).
(1)求tan∠OPQ的值;
(2)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
【答案】
(1)解:∵y=x2﹣2x+1=(x﹣1)2
∴顶点P(1,0),
∵当x=0时,y=1,
∴Q(0,1),
∴tan∠OPQ=1;
(2)解:①设抛物线C′的解析式为y=x2﹣2x+m,
∴Q′(0,m)其中m>1,
∴OQ′=m,
∵F(1, ![]() ),
),
过F作FH⊥OQ′,如图:
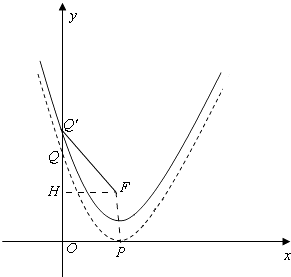
∴FH=1,Q′H=m﹣ ![]() ,
,
在Rt△FQ′H中,FQ′2=(m﹣ ![]() )2+1=m2﹣m+
)2+1=m2﹣m+ ![]() ,
,
∵FQ′=OQ′,
∴m2﹣m+ ![]() =m2,
=m2,
∴m= ![]() ,
,
∴抛物线C′的解析式为y=x2﹣2x+ ![]() ,
,
②方法一:设点A(x0,y0),则y0=x02﹣2x0+ ![]() ①,
①,
过点A作x轴的垂线,与直线Q′F相交于点N,则可设N(x0,n),
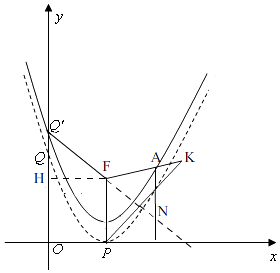
∴AN=y0﹣n,其中y0>n,
连接FP,
∵F(1, ![]() ),P(1,0),
),P(1,0),
∴FP⊥x轴,
∴FP∥AN,
∴∠ANF=∠PFN,
连接PK,则直线Q′F是线段PK的垂直平分线,
∴FP=FK,有∠PFN=∠AFN,
∴∠ANF=∠AFN,则AF=AN,
∵A(x0,y0),F(1, ![]() ),
),
∴AF2=(x0﹣1)2+(y0﹣ ![]() )2=x02﹣2x0+1+y02﹣y0+
)2=x02﹣2x0+1+y02﹣y0+ ![]() =x02﹣2x0+
=x02﹣2x0+ ![]() +y02﹣y0=(x02﹣2x0+
+y02﹣y0=(x02﹣2x0+ ![]() )+y02﹣y0②
)+y02﹣y0②
∵y0=x02﹣2x0+ ![]() ①,
①,
将①右边整体代换②得,AF2=(x02﹣2x0+ ![]() )+y02﹣y0=y0+y02﹣y0=y02
)+y02﹣y0=y0+y02﹣y0=y02
∵y0>0
∴AF=y0,
∴y0=y0﹣n,
∴n=0,
∴N(x0,0),
设直线Q′F的解析式为y=kx+b,
则 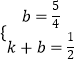 ,
,
解得 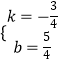 ,
,
∴y=﹣ ![]() x+
x+ ![]() ,
,
由点N在直线Q′F上,得,0=﹣ ![]() x0+
x0+ ![]() ,
,
∴x0= ![]() ,
,
将x0= ![]() 代入y0=x
代入y0=x ![]() ﹣2x0+
﹣2x0+ ![]() ,
,
∴y0= ![]() ,
,
∴A( ![]() ,
, ![]() ).
).
方法二:由①有,Q'(0, ![]() ),F(1,
),F(1, ![]() ),P(1,0),
),P(1,0),
∴直线FQ'的解析式为y=﹣ ![]() x+
x+ ![]() ①,
①,
∵FQ'⊥PK,P(1,0),
∴直线PK的解析式为y= ![]() x﹣
x﹣ ![]() ②
②
联立①②得出,直线FQ'与PK的交点M坐标为( ![]() ,
, ![]() ),
),
∵点P,K关于直线FQ'对称,
∴K( ![]() ,
, ![]() ),
),
∵F(1, ![]() ),
),
∴直线FK的解析式为y= ![]() x+
x+ ![]() ③,
③,
∵射线FK与抛物线C′:y=x2﹣2x+ ![]() ④相交于点A,
④相交于点A,
∴联立③④得, 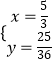 或
或 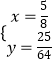 (舍),
(舍),
∴A( ![]() ,
, ![]() ).
).
【解析】(1)配成顶点式,求出顶点坐标,利用正切定义,求出正切;(2)抛物线上下平移,解析式整体上加减常数m,由FQ′=OQ′,利用勾股定理构建方程,求出m;由"P关于直线Q′F的对称点为K,“可利用轴对称的性质,得出直线Q′F是线段PK的垂直平分线,以A的横、纵坐标为未知数建立两个方程y0=x02﹣2x0+ 5 4 ①,0=﹣ ![]() x0+
x0+ ![]() ,求出坐标.
,求出坐标.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:初中数学 来源: 题型:
【题目】分如图,在ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.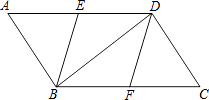
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON = 50°,OE 平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D、设∠OAC = x°.
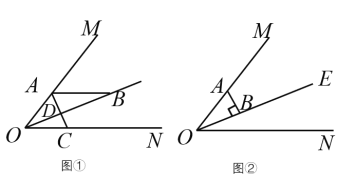
(1)如图①,若AB//ON,
①则∠ABO 的度数是________;
②当∠BAD =∠ABD 时,x=_______;当∠BAD = ∠BDA 时,x=________.
(2)如图②,若AB⊥OE,则是否存在这样的x值,使得 △ABD 中有一个角是另一个角的两倍.存在,直接写出x的值;不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中、∠BAD=120°,点O为射线CA 上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.
(1)如图①,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA三条段段之间的数量关系;
(2)如图②,点O在CA的延长线上,且OA=![]() AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;
AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;
(3)点O在线段AC上,若AB=6,BO=2![]() ,当CF=1时,请直接写出BE的长.
,当CF=1时,请直接写出BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年某企业按餐厨垃圾处理费50元/吨、建筑垃圾处理费20元/吨的收费标准,共支付餐厨和建筑垃圾处理费7000元.从2016年元月起,收费标准上调为:餐厨垃圾处理费120元/吨,建筑垃圾处理费40元/吨.若该企业2016年处理的这两种垃圾数量与2015年相比没有变化,就要多支付垃圾处理费8600元.
(1)该企业2015年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2016年将上述两种垃圾处理总量减少到200吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2016年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com