
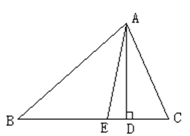
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=44°,∠DAE=15°,求∠C的度数.
【答案】74°
【解析】
由AD是BC边上的高线知∠ADE=90°,∠DAE=15°可计算出∠AED=75°,根据内外角关系可求出∠BAE=31°,根据角平分线的性质可求出∠BAC=62°,最后在△ABC中,根据内角和定理即可求出∠C的度数.
解: ∵AD是BC边上的高,∠DAE=15°,
∴∠ADE=90°,
∵∠ADE+∠AED+∠DAE=180°, ∠DAE=15°,
∴∠AED=180°- ∠ADE-∠DAE=180°- 90°- 15°=75°,
∵∠B+∠BAE=∠AED, ∠B=44°,
∴∠BAE=∠AED-∠B=75°- 44°=31°,
∵AE是∠BAC平分线,
∴∠BAC=2∠BAE=2×31°= 62° ,
∵∠B+∠BAC+∠C=180°,
∴∠C=180°- ∠B - ∠BAC=180°- 44° - 62°=74°.
故答案为:74°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
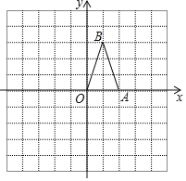
【题目】如图,在平面直角坐标系中,已知点A(2,0),点B(1,3).
(1)画出将△OAB绕原点顺时针旋转90°后所得的△OA1B1,并写出点A1,B1的坐标;
(2)画出△OAB关于原点O的中心对称图形△OA2B2,并写出点A2,B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两个码头分别在一条河的两岸AC、BD上,河岸AC、BD均为东西走向,一艘客轮以每小时30千米的速度由A码头出发沿北偏东50°的方向航行至B码头,用时1.2小时,求该河的宽度(结果精确到1千米)
【参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20】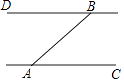
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )
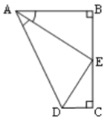
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知动点P以每秒2㎝的速度沿图甲的边框按从![]() 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:

(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙的b是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1, ![]() ).
).
(1)求tan∠OPQ的值;
(2)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市组织学术研讨会,需租用客车接送参会人员往返宾馆和观摩地点,客车租赁公司现有![]() 座和
座和![]() 座两种型号的客车可供租用.
座两种型号的客车可供租用.
(1)已知![]() 座的客车每辆每天的租金比
座的客车每辆每天的租金比![]() 座的贵
座的贵![]() 元,会务组第一天在这家公司租了
元,会务组第一天在这家公司租了![]() 辆
辆![]() 座和
座和![]() 辆
辆![]() 座的客车.一天的租金为
座的客车.一天的租金为![]() 元,求
元,求![]() 座和
座和![]() 座的客车每辆每天的租金各是多少元?
座的客车每辆每天的租金各是多少元?
(2)由于第二天参会人员发生了变化,因此会务纽需重新确定租车方案.
方案1:若只租用![]() 座的客车,会有一辆客车空出
座的客车,会有一辆客车空出![]() 个座位;
个座位;
方案2:若只租用![]() 座客车,正好坐满且比只租用
座客车,正好坐满且比只租用![]() 座的客车少用两辆.
座的客车少用两辆.
①请计算方案1、2的费用;
②从经济角度考虑,还有方案3吗?如果你是会务纽负责人,应如何确定最终租车方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com