
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧСтаЮABCDЕФСНЬѕЖдНЧЯпГЄКЭБпГЄЃЌетЪБЮвУЧАбЙигк
ЗжБ№ЪЧСтаЮABCDЕФСНЬѕЖдНЧЯпГЄКЭБпГЄЃЌетЪБЮвУЧАбЙигк![]() ЕФаЮШчЁА
ЕФаЮШчЁА![]() ЁБЕФвЛдЊЖўДЮЗНГЬГЦЮЊЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБЃЎЧыНтОіЯТСаЮЪЬтЃК
ЁБЕФвЛдЊЖўДЮЗНГЬГЦЮЊЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБЃЎЧыНтОіЯТСаЮЪЬтЃК
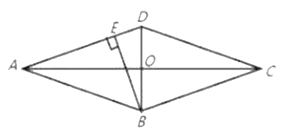
ЃЈ1ЃЉЬюПеЃКЂйЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ
ЃЎ
ЂкгУКЌ![]() ЃЌ
ЃЌ![]() ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО![]() жЕЃЌ
жЕЃЌ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЧѓжЄЃКЙигк![]() ЕФЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ
ЕФЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ![]() БигаЪЕЪ§ИљЃЛ
БигаЪЕЪ§ИљЃЛ
ЃЈ3ЃЉШє![]() ЪЧЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ
ЪЧЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ![]() ЕФвЛИіИљЃЌЧвСтаЮЕФУцЛ§ЪЧ25ЃЌBEЪЧСтаЮABCDЕФADБпЩЯЕФИпЃЌЧѓBEЕФжЕЃЎ
ЕФвЛИіИљЃЌЧвСтаЮЕФУцЛ§ЪЧ25ЃЌBEЪЧСтаЮABCDЕФADБпЩЯЕФИпЃЌЧѓBEЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй5ЃЌЂк![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНсКЯЭМаЮЃЌИљОнСтаЮЕФЖдНЧЯпЛЅЯрЦНЗжвдМАЙДЙЩЖЈРэМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉЫуГіЁїЃЌНсКЯЃЈ1ЃЉжаЂкЕФНсТлМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉИљОнЗНГЬИљЕФЖЈвхЕУГіmЁЂnЁЂtЕФЙиЯЕЃЌНсКЯЃЈ1ЃЉжаЂкЕФНсТлНјааЛЏМђЃЌдйИљОнСтаЮУцЛ§ЪЧ25ЃЌМДПЩЕУГіtЕФжЕЃЌНјЖјЕУГіНсТлЃЎ
ЃЈ1ЃЉЂйЕБm=6ЃЌn=8ЪБЃЌAO=4ЃЌOB=3ЃЌЁрt=AB=![]() =5ЃЎ
=5ЃЎ
ЂкЁпAO=![]() ЃЌOB=
ЃЌOB=![]() ЃЌЁрt2=AB2=
ЃЌЁрt2=AB2=![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК5ЃЌ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉ![]()
етРяЃЌa=mЃЌb=![]() tЃЌc=nЃЌЁр
tЃЌc=nЃЌЁр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌЁр
ЃЌЁр![]()
![]() ЃЌЁрЙигк
ЃЌЁрЙигк![]() ЕФЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ
ЕФЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ![]() БигаЪЕЪ§ИљЃЎ
БигаЪЕЪ§ИљЃЎ
ЃЈ3ЃЉЁп![]() ЪЧЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ
ЪЧЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ![]() ЕФвЛИіИљЃЌЁр
ЕФвЛИіИљЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌЁр
ЃЌЁр![]() ЃЎ
ЃЎ
ЁпСтаЮУцЛ§ЪЧ25ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌМД
ЃЌМД![]() ЃЌЁр
ЃЌЁр![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЕуPЪЧABБпЩЯвЛЕу![]() ВЛгыAЃЌBжиКЯ
ВЛгыAЃЌBжиКЯ![]() ЃЌ
ЃЌ![]() ЃЌЙ§Еузї
ЃЌЙ§Еузї![]() ЃЌНЛADБпгкЕуQЃЌСЌНсCQЃЎ
ЃЌНЛADБпгкЕуQЃЌСЌНсCQЃЎ
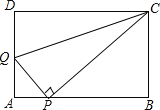
![]() Шє
Шє![]() ЃЌЧѓжЄЃКЫФБпаЮABCDЪЧОиаЮЃЛ
ЃЌЧѓжЄЃКЫФБпаЮABCDЪЧОиаЮЃЛ
![]() дк
дк![]() ЕФЬѕМўЯТЃЌЕБ
ЕФЬѕМўЯТЃЌЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЧѓAQЕФГЄЃЎ
ЪБЃЌЧѓAQЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
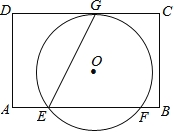
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAD=8ЃЌEЪЧБпABЩЯвЛЕуЃЌЧвAE=![]() ABЃЌЁбOОЙ§ЕуEЃЌгыБпCDЫљдкжБЯпЯрЧагкЕуGЃЈЁЯGEBЮЊШёНЧЃЉЃЌгыБпABЫљдкжБЯпЯрНЛгкСэвЛЕуFЃЌЧвEGЃКEF=
ABЃЌЁбOОЙ§ЕуEЃЌгыБпCDЫљдкжБЯпЯрЧагкЕуGЃЈЁЯGEBЮЊШёНЧЃЉЃЌгыБпABЫљдкжБЯпЯрНЛгкСэвЛЕуFЃЌЧвEGЃКEF=![]() .ЕББпADЛђBCЫљдкЕФжБЯпгыЁбOЯрЧаЪБЃЌABЕФГЄЪЧ .
.ЕББпADЛђBCЫљдкЕФжБЯпгыЁбOЯрЧаЪБЃЌABЕФГЄЪЧ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЁбOЪЧЁїABCЕФЭтНгдВЃЌЕуMЮЊЁбOЩЯвЛЕу.
ЃЈ1ЃЉШчЭМЃЌШєЁїABCЮЊЕШБпШ§НЧаЮЃЌBM=1ЃЌCM=2ЃЌЧѓAMЕФГЄЃЛ

аЁУїдкНтОіетИіЮЪЬтЪБВЩгУЕФЗНЗЈЪЧЃКбгГЄMCЕНEЃЌЪЙME=AMЃЌДгЖјПЩжЄЁїAMEЮЊЕШБпШ§НЧаЮЃЌВЂЧвЁїABMЁеЁїACEЃЌНјЖјОЭПЩЧѓГіЯпЖЮAMЕФГЄЃЎ
ЧыФуНшМјаЁУїЕФЗНЗЈаДГіAMЕФГЄЃЌВЂаДГіЭЦРэЙ§ГЬЃЎ
ЃЈ2ЃЉШєЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=90ЁуЃЌ![]() ЃЌЃЈЦфжаbЃОaЃЉЃЌжБНгаДГіAMЕФГЄ(гУКЌгаaЃЌbЕФДњЪ§ЪНБэЪО).
ЃЌЃЈЦфжаbЃОaЃЉЃЌжБНгаДГіAMЕФГЄ(гУКЌгаaЃЌbЕФДњЪ§ЪНБэЪО).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌEЪЧABБпЩЯвЛЕуЃЌЧвЁЯA=ЁЯEDF=60ЁуЃЌгаЯТСаНсТлЃКЂйAE=BFЃЛЂкЁїDEFЪЧЕШБпШ§НЧаЮЃЛЂлЁїBEFЪЧЕШбќШ§НЧаЮЃЛЂмЁЯADE=ЁЯBEFЃЌЦфжаНсТле§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ

A.3
B.4
C.1
D.2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦяздааГЕТУаадНРДдНЪмЕНШЫУЧЕФЯВАЎЃЌИїжжЦЗХЦЕФЩНЕиздааГЕЯрМЬЭЖЗХЪаГЁЃЌЫГЗчГЕааОгЊЕФ![]() аЭГЕШЅФъ6дТЗнЯњЪлзмЖюЮЊ3.2ЭђдЊЃЌНёФъОЙ§ИФдьЩ§МЖКѓ
аЭГЕШЅФъ6дТЗнЯњЪлзмЖюЮЊ3.2ЭђдЊЃЌНёФъОЙ§ИФдьЩ§МЖКѓ![]() аЭГЕУПСОЯњЪлМлБШШЅФъдіМг400дЊЃЌШєНёФъ6дТЗнгыШЅФъ6дТЗнТєГіЕФ
аЭГЕУПСОЯњЪлМлБШШЅФъдіМг400дЊЃЌШєНёФъ6дТЗнгыШЅФъ6дТЗнТєГіЕФ![]() аЭГЕЪ§СПЯрЭЌЃЌдђНёФъ6дТЗн
аЭГЕЪ§СПЯрЭЌЃЌдђНёФъ6дТЗн![]() аЭГЕЯњЪлзмЖюНЋБШШЅФъ6дТЗнЯњЪлзмЖюдіМг
аЭГЕЯњЪлзмЖюНЋБШШЅФъ6дТЗнЯњЪлзмЖюдіМг![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ![]() СНжжаЭКХГЕЕФНјЛѕКЭЯњЪлМлИёБэЃК
СНжжаЭКХГЕЕФНјЛѕКЭЯњЪлМлИёБэЃК
|
| |
НјЛѕМлИёЃЈдЊ | 1100 | 1400 |
ЯњЪлМлИёЃЈдЊ | НёФъЕФЯњЪлМлИё | 2400 |
ЃЈ1ЃЉЧѓНёФъ6дТЗн![]() аЭГЕУПСОЯњЪлМлЖрЩйдЊЃЛ
аЭГЕУПСОЯњЪлМлЖрЩйдЊЃЛ
ЃЈ2ЃЉИУГЕааМЦЛЎ7дТЗнаТНјвЛХњ![]() аЭГЕКЭ
аЭГЕКЭ![]() аЭГЕЙВ50СОЃЌЧв
аЭГЕЙВ50СОЃЌЧв![]() аЭГЕЕФНјЛѕЪ§СПВЛГЌЙ§
аЭГЕЕФНјЛѕЪ§СПВЛГЌЙ§![]() аЭГЕЪ§СПЕФСНБЖЃЌгІШчКЮНјЛѕВХФмЪЙетХњГЕЛёРћзюЖрЃП
аЭГЕЪ§СПЕФСНБЖЃЌгІШчКЮНјЛѕВХФмЪЙетХњГЕЛёРћзюЖрЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮAEHCЪЧгЩШ§ИіШЋЕШОиаЮЦДГЩЕФЃЌAHгыBEЁЂBFЁЂDFЁЂDGЁЂCGЗжБ№НЛгкЕуPЁЂQЁЂKЁЂMЁЂNЃЎЩшЁїBPQЃЌЁїDKMЃЌЁїCNHЕФУцЛ§вРДЮЮЊS1ЃЌS2ЃЌS3ЃЎШєS1+S3ЃН20ЃЌдђS2ЕФжЕЮЊЃЈЁЁЁЁЃЉ

A. 6 B. 8 C. 10 D. 12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФЗНГЬЃЈkЉ1ЃЉx2+2kx+2=0ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЮоТлkЮЊКЮжЕЃЌЗНГЬзмгаЪЕЪ§ИљЃЎ
ЃЈ2ЃЉЩшx1ЃЌx2ЪЧЗНГЬЃЈkЉ1ЃЉx2+2kx+2=0ЕФСНИіИљЃЌМЧ![]() ЃЌSЕФжЕФмЮЊ2Т№ЃПШєФмЃЌЧѓГіДЫЪБkЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЃЌSЕФжЕФмЮЊ2Т№ЃПШєФмЃЌЧѓГіДЫЪБkЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙЄШЫЪІИЕЭЏЭўзМБИдквЛПщГЄЮЊ60ЃЌПэЮЊ48ЕФГЄЗНаЮЛЈЦдФкаоНЈЫФЬѕПэЖШЯрЕШЃЌЧвгыИїБпДЙжБЕФаЁТЗЃЎЫФЬѕаЁТЗЮЇГЩЕФжаМфВПЗжЧЁКУЪЧвЛИіе§ЗНаЮЃЌЧвБпГЄЪЧаЁТЗПэЖШЕФ8БЖЃЎШєЫФЬѕаЁТЗЫљеМУцЛ§ЮЊ160ЃЎЩшаЁТЗЕФПэЖШЮЊxЃЌвРЬтвтСаЗНГЬЃЌЛЏЮЊвЛАуаЮЪНЮЊ_________
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com