练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

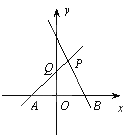
    【题目】如图，直线PA是一次函数y=x+1的图象，直线PB是一次函数y=-2x+2的图象.

    （1）求A、B、P三点的坐标；

    （2）求四边形PQOB的面积；

    【答案】(1)P(,)；（2）.

    【解析】试题分析：（1）令一次函数y=x+1与一次函数y=﹣2x+2的y=0可分别求出A，B的坐标，再由可求出点P的坐标；

    （2）根据四边形PQOB的面积=S△BOM﹣S△QPM即可求解．

    解：（1）∵一次函数y=x+1的图象与x轴交于点A，∴A（﹣1，0），

    一次函数y=﹣2x+2的图象与x轴交于点B，∴B（1，0），

    由，解得，∴P（，）．

    （2）设直线PA与y轴交于点Q，则Q（0，1），直线PB与y轴交于点M，则M（0，2），

    ∴四边形PQOB的面积=S△BOM﹣S△QPM=×1×2﹣×1×=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲乙两地相距200千米，一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，相向而行.已知客车的速度为60千米/小时，出租车的速度是100千米/小时.

    （1）多长时间后两车相遇？

    （2）若甲乙两地之间有相距50km的A、B两个加油站，当客车进入A站加油时，出租车恰好进入B站加油，求A加油站到甲地的距离.

    （3）若出租车到达甲地休息10分钟后，按原速原路返回.出租车能否在到达乙地或到达乙地之前追上客车？若不能，则出租车往返的过程中，至少提速为多少才能在到达乙地或到达乙地之前追上客车？是否超速（高速限速为120千米/小时）？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为丰富学生的校园生活，准备从某体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买3个足球和2个篮球共需310元，购买2个足球和5个篮球共需500元．
    （1）购买一个足球，一个篮球各需多少元？
    （2）根据学校的实际情况，需从该体育用品商店一次性购买足球和篮球共96个，要求购买足球和篮球的总费用不超过5720元，这所中学最多可以购买多少个篮球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩．根据统计图中的信息可得，下列结论正确的是（　　）

    A. 甲队员成绩的平均数比乙队员的大

    B. 甲队员成绩的方差比乙队员的大

    C. 甲队员成绩的中位数比乙队员的大

    D. 乙队员成绩的方差比甲队员的大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场经营A种品牌的玩具，购进时间的单价是30元，但据市场调查，在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．
    （1）不妨设该种品牌玩具的销售单价为x元（x＞40），请用含x的代数式表示该玩具的销售量；
    （2）若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于450件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？
    （3）该商场计划将（2）中所得的利润的一部分资金采购一批B种玩具并转手出售，根据市场调查并准备两种方案，方案①：如果月初出售，可获利15%，并可用本和利再投资C种玩具，到月末又可获利10%；方案②：如果只到月末出售可直接获利30%，但要另支付他库保管费350元，请问商场如何使用这笔资金，采用哪种方案获利较多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，点E.F分别在AB、CD上，AE=CF，连接AF，BF，DE，CE，分别交于H、G.

    求证：(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

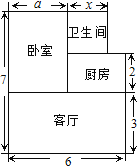
    【题目】张先生准备在沙坪坝购买一套小户型商品房，他去某楼盘了解情况得知，该户型商品房的单价是12000元/m2，面积如图所示（单位：米，卧室的宽为a米，卫生间的宽为x米），

    (1) 用含a和x的式子表示该户型的面积

    (2) 售房部为张先生提供了以下两种优惠方案：

    方案一：整套房的单价是12 000元/m2，其中厨房只算的面积;

    方案二：整套房按原销售总金额的9折出售,

    若张先生购买的户型a＝3，且分别用两种方案购房金额相等，求x的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，点A（0，4），B（﹣3，4），C（﹣6，0），动点P从点A出发以1个单位/秒的速度在y轴上向下运动，动点Q同时从点C出发以2个单位/秒的速度在x轴上向右运动，过点P作PD⊥y轴，交OB于D，连接DQ．当点P与点O重合时，两动点均停止运动．设运动的时间为t秒．

    （1）当t=1时，求线段DP的长；
    （2）连接CD，设△CDQ的面积为S，求S关于t的函数解析式，并求出S的最大值；
    （3）运动过程中是否存在某一时刻，使△ODQ与△ABC相似？若存在，请求出所有满足要求的t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（ ）

    A.7
    B.8
    C.9
    D.10

    查看答案和解析>>

    同步练习册答案