
����Ŀ�������������200ǧ�ף�һ���ͳ��Ӽؿ����ҵأ�һ��������ҵؿ����أ�����ͬʱ�������������.��֪�ͳ����ٶ�Ϊ60ǧ��/Сʱ��������ٶ���100ǧ��/Сʱ.
��1���ʱ�������������
��2������������֮�������50km��A��B��������վ�����ͳ�����Aվ����ʱ�����ǡ�ý���Bվ���ͣ���A����վ���صľ���.
��3��������������Ϣ10���Ӻ�ԭ��ԭ·����.����ܷ��ڵ����ҵػ��ҵ�֮ǰ�Ͽͳ��������ܣ����������Ĺ����У���������Ϊ���ٲ����ڵ����ҵػ��ҵ�֮ǰ�Ͽͳ����Ƿ��٣���������Ϊ120ǧ��/Сʱ����Ϊʲô��
���𰸡���1��2.5����2��112.5km��187.5km ����3�����ܣ� ![]() ����.
����.
��������
���⣨1����xСʱ�������������ݿͳ���·��+�����·��=400�з��̽�����⼴�ɵã�
��2����A����վ�ڼ���B����վ֮�䣬B����վ�ڼ���A����վ֮����������г�������⼴����
��3������������Ϣ40����ʱ�ͳ�����ʻ��280ǧ�ף��ͳ������ҵػ���Ҫ2Сʱ��
100��2=200<400����˳�������ڵ����ҵػ��ҵ�֮ǰ�Ͽͳ����������ٺ���ٶ�Ϊyǧ��/ʱ������������в���ʽΪ![]() ���ⲻ��ʽ�������жϼ��ɵ�.
���ⲻ��ʽ�������жϼ��ɵ�.
�����������1����xСʱ�����������������⣬����
60x+100x=400��
��ã�x=2.5��
��2.5Сʱ������������
��2����ͳ���A����վ�õ�ʱ����xСʱ��������B����վ��ʱ��Ҳ��xСʱ��
A����վ��صľ�����60xǧ����
����������60x+100x=400-100��60x+100x=400+100��
��ã�x=![]() ��x=
��x=![]() ��
��
����60x=112.5��60x=187.5��
��A����վ���صľ�����112.5km��187.5km��
��3��������������ʱ��400��100=4Сʱ����Ϣ40���ӣ�
��ʱ�ͳ�����ʻ��60����4+![]() ��=280ǧ�ף� �������ͳ��ľ�����280ǧ�ף�
��=280ǧ�ף� �������ͳ��ľ�����280ǧ�ף�
�ͳ������ҵػ���Ҫ��400-280����60=2Сʱ��
100��2=200<400����˳�������ڵ����ҵػ��ҵ�֮ǰ�Ͽͳ���
�������ٺ���ٶ�Ϊyǧ��/ʱ������![]() ��
��
��ã�y![]() ��
��
![]() >120�����Գ��٣�
>120�����Գ��٣�
�𣺳�������Ĺ����У��ٶ�����Ϊ![]() ǧ��/ʱ�����ڵ����ҵػ��ҵ�֮ǰ�Ͽͳ�����ʱ����.
ǧ��/ʱ�����ڵ����ҵػ��ҵ�֮ǰ�Ͽͳ�����ʱ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧѧ����Ϊ�˽��Уѧ��ϲ���������������ȡ��������ķ�����������ƹ��������������ĸ����������������ѧ������Ȥ���ã���������Ľ�����Ƴ����µ�������������ͳ��ͼ����Ҫ��ÿλͬѧֻ��ѡ��һ���Լ�ϲ�������ࣻ����ͳ��ͼ����ƹ�������������������ϲ�������������е�ijһ�������ѧ���������������ͼ���ṩ����Ϣ������������⣺
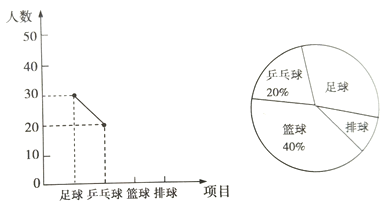
��1��������о��У�һ�������˶�����ѧ����
��2��ϲ�����������������ͳ��ͼ������Ӧ�����ε�Բ�Ľ��Ƕ��ٶȣ�
��3����ȫƵ���ֲ�����ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���� ![]() Ϊһ����ֱ��ϸ�ߣ�A��B������
Ϊһ����ֱ��ϸ�ߣ�A��B������ ![]() �ϣ���
�ϣ��� ![]() ��
�� ![]() =1��3��
=1��3�� ![]() ��
�� ![]() =3��5�����ȹ̶�B�㣬��
=3��5�����ȹ̶�B�㣬�� ![]() ����
���� ![]() ��ʹ��
��ʹ�� ![]() �ص���
�ص��� ![]() �ϣ���ͼ���������ٴ�ͼ������ ��A�㼰��A���ص���һ�������ʹ��ϸ�߷ֳ����Σ��������ϸ����С����ij��ȱ�Ϊ�Σ�������
�ϣ���ͼ���������ٴ�ͼ������ ��A�㼰��A���ص���һ�������ʹ��ϸ�߷ֳ����Σ��������ϸ����С����ij��ȱ�Ϊ�Σ������� 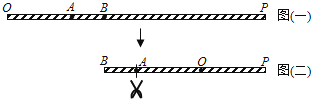
A.1��1��1
B.1��1��2
C.1��2��2
D.1��2��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ���ͬ�IJ�Ϊ����������ij��������������.
�磺2��2��2��(-3)��(-3)��(-3 )��( -3)��. ����������ij˷������ǰ� 2��2��2 ���� 2����������2 ��Ȧ 3 �η���. (-3)��(-3)��(-3 )��( -3)����(-3)����������-3 ��Ȧ 4 �η���.
һ��أ���![]() ��a��0������
��a��0������![]() ��������a��Ȧn�η���.
��������a��Ȧn�η���.
(1)ֱ��д���������� ![]() _____��
_____�� ![]() _________��
_________�� ![]() ___________��
___________��
(2)����֪�����������ļ����������ת��Ϊ�ӷ������������������ת��Ϊ�˷�������
�볢�Խ��������ij�������ת��Ϊ�˷�����������������һ��������������Ȧ n �η�����_____.
(3)���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪����������A��B��Ӧ�����ֱ��ǩ�1��3����PΪ�����ϵ�һ���㣬���Ӧ����Ϊx

��1��A��B����ľ���AB=�� ����
��2�����������Ƿ���ڵ�P��ʹPA+PB=6�������ڣ������x��ֵ���������ڣ���˵�����ɣ�
��3����ͼ2������P��ÿ��1����λ���ٶȴӵ�O���������˶���ͬʱ��A��ÿ��5����λ���ٶ������˶�����B��ÿ��20����λ���ٶ������˶������˶��Ĺ����У�M��N�ֱ���AP��OB���е㣬�ʣ�![]() ��ֵ�Ƿ����仯����˵�����ɣ�
��ֵ�Ƿ����仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������»��������Ϧ������£������б�ʾ���µ���ǵ�ʽ���У���90�㩁�Ϧ£��ڡϦ���90�㣻��![]() ���Ϧ�+�Ϧ£�����
���Ϧ�+�Ϧ£�����![]() ���Ϧ������£������д�����У���������
���Ϧ������£������д�����У���������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����a1��a2��a3��a4������������������a1=0��a2=��|a1+1|��a3=��|a2+2|��a4=��|a3+3|�������������ƣ���a2018��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��F��C��E��ֱ��l����F��C֮�䲻��ֱ�Ӳ���������A��D��l��࣬���AB=DE��AC=DF��BF=EC.

��1����֤����ABC�ա�DEF��
��2��ָ��ͼ������ƽ�е��߶Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ�߶�AB�ӳ�����һ�㣬DΪ�߶�BC��һ�㣬CD��2BD��EΪ�߶�AC��һ�㣬CE��2AE
![]()
(1)��AB��18��BC��21����DE�ij���
(2)��AB��a����DE�ij���(�ú�a�Ĵ���ʽ��ʾ)
(3)��ͼ�������߶εij���֮�����߶�AD���ȵ�7������![]() ��ֵΪ�� ����
��ֵΪ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com