
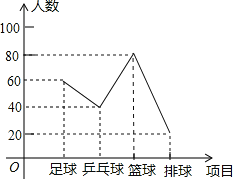
【题目】某中学学生会为了解该校学生喜欢球类活动的情况,采取抽样调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成如下的两幅不完整的统计图。(要求每位同学只能选择一种自己喜欢的球类;扇形统计图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数)请你根据图中提供的信息,解答下列问题:
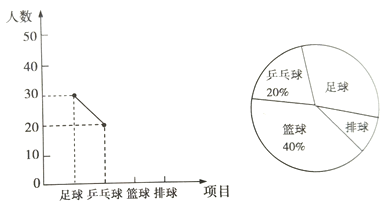
(1)在这次研究中,一共调查了多少名学生?
(2)喜欢排球的人数在扇形统计图中所对应的扇形的圆心角是多少度?
(3)补全频数分布折线统计图。
【答案】见解析
【解析】
试题(1)根据喜欢乒乓球的人数是20人,占20%,即可求得总人数,然后即可求得喜欢足球的人数的百分率;
(2)喜欢排球的人所占的百分比是1减去喜欢其他所有项目的百分比,然后乘以360°即可得到扇形统计图中所占的圆心角;
(3)求得喜欢篮球的人数与喜欢排球的人数即可作出统计图.
试题解析:(1)总人数是:20÷20%=100人,喜欢足球的人数的百分率是:![]() ×100%=30%;
×100%=30%;
(2)喜欢排球的人所占的百分比是:1-20%-40%-30%=10%,则在扇形统计图中所占的圆心角360×10%=36°;
(3)喜欢篮球的人数是:200×40%=80人,喜欢排球的人数是:200×10%=20人.


科目:初中数学 来源: 题型:
【题目】已知一个三角形的两条边长分别是1cm和2cm,一个内角为![]() .
.

(1)请你借助图1画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在图1的右边用“尺规作图”作出所有这样的三角形;若不能,请说明理由.
(3)如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为![]() ”,那么满足这一条件,且彼此不全等的三角形共有 个.
”,那么满足这一条件,且彼此不全等的三角形共有 个.
友情提醒:请在你画的图中标出已知角的度数和已知边的长度,“尺规作图”不要求写作法,但要保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
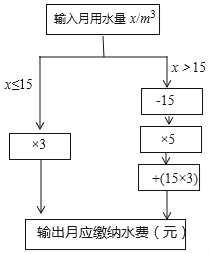
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( ) 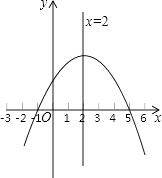
A.ac<0
B.a﹣b+c>0
C.b=﹣4a
D.关于x的方程ax2+bx+c=0的根是x1=﹣1,x2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2012~2016年常住人口数统计如图所示。
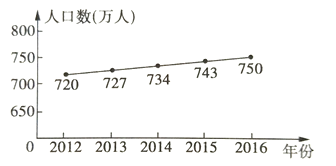
(1)该市常住人口数2016年比2015年增加了___________万人;
(2)与上一年相比,该市常住人口数增长率最大的年份是__________________;
(3)预测2017年该市常住人口大约有多少万人,并用所学的统计知识说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2﹣x﹣3.
(1)求函数图象的顶点坐标,与坐标轴交点坐标,并画出函数大致图象; 
(2)根据图象直接回答:当x为何值时,y<0?当x为何值时y>﹣3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3,4,5;5,12,13;7,24,25;9,40,41;……发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数:_______________________;
(2)若第一个数用字母n(n为奇数,且n≥3)表示,则后两个数用含n的代数式表示分别为___________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B两个点.
(1)如图1,若AB=a,M是AB的中点,C为线段AB上的一点,且![]() ,则AC= ,CB= ,MC= (用含a的代数式表示);
,则AC= ,CB= ,MC= (用含a的代数式表示);
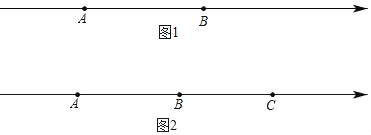
(2)如图2,若A、B、C三点对应的数分别为﹣40,﹣10,20.
①当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段AB的中点,点N为线段BC的中点,在B、C相遇前,在运动多少秒时恰好满足:MB=3BN.
②现有动点P、Q都从C点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到B点时,点Q才从C点出发,并以每秒3个单位长度的速度向左移动,且当点P到达A点时,点Q也停止移动(若设点P的运动时间为t).当PQ两点间的距离恰为18个单位时,求满足条件的时间t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距200千米,一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,相向而行.已知客车的速度为60千米/小时,出租车的速度是100千米/小时.
(1)多长时间后两车相遇?
(2)若甲乙两地之间有相距50km的A、B两个加油站,当客车进入A站加油时,出租车恰好进入B站加油,求A加油站到甲地的距离.
(3)若出租车到达甲地休息10分钟后,按原速原路返回.出租车能否在到达乙地或到达乙地之前追上客车?若不能,则出租车往返的过程中,至少提速为多少才能在到达乙地或到达乙地之前追上客车?是否超速(高速限速为120千米/小时)?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com