
����Ŀ����֪��������A��B�����㣮
��1����ͼ1����AB=a��M��AB���е㣬CΪ�߶�AB�ϵ�һ�㣬��![]() ����AC=�� ����CB=�� ����MC=�� �����ú�a�Ĵ���ʽ��ʾ����
����AC=�� ����CB=�� ����MC=�� �����ú�a�Ĵ���ʽ��ʾ����
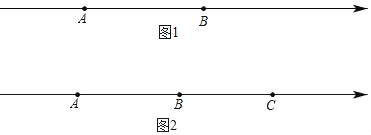
��2����ͼ2����A��B��C�����Ӧ�����ֱ�Ϊ��40����10��20��
����A��C����ͬʱ�����˶���ͬʱB�������˶�����֪��A��B��C���ٶȷֱ�Ϊ8����λ����/�롢4����λ����/�롢2����λ����/�룬��MΪ�߶�AB���е㣬��NΪ�߶�BC���е㣬��B��C����ǰ�����˶�������ʱǡ�����㣺MB=3BN��
�����ж���P��Q����C���������P��ÿ��1����λ���ȵ��ٶ����յ�A�ƶ�������P�ƶ���B��ʱ����Q�Ŵ�C�����������ÿ��3����λ���ȵ��ٶ������ƶ����ҵ���P����A��ʱ����QҲֹͣ�ƶ��������P���˶�ʱ��Ϊt������PQ�����ľ���ǡΪ18����λʱ��������������ʱ��tֵ��
���𰸡���1��![]() a��
a��![]() a��
a��![]() a����2��2��ʱǡ������MB=3BN����3����tΪ18�롢36���54��ʱ��P��Q�������18����λ���ȣ�
a����2��2��ʱǡ������MB=3BN����3����tΪ18�롢36���54��ʱ��P��Q�������18����λ���ȣ�
��������
��1�����������еĵ�����ϵ��a��ʾ��AC,CB,MC���ɣ�
��2���ټ���x��C��B�ұ�ʱ��ǡ������MB=3BN���ݴ˵ó����̣����x��ֵ���ɣ�
�ڵ�P��ʾ����Ϊ20��t����Q��ʾ����Ϊ20��3��t��30�����ٷ�������ۢٵ���P�ƶ�18��ʱ���ڵ�Q�ڵ�P���Ҳ࣬�۵���Q�ڵ�P����࣬���ɵó�����.
�⣺��1����AB=a��CΪ�߶�AB�ϵ�һ�㣬��![]() =
=![]() ��
��
��AC=![]() AB=
AB=![]() a��CB=
a��CB=![]() AB=
AB=![]() a��
a��
��M��AB���е㣬
��MC=![]() AB��
AB��![]() AB=
AB=![]() a��
a��
�ʴ�Ϊ��![]() a��
a��![]() a��
a��![]() a��
a��
��2������A��B��C�����Ӧ�����ֱ�Ϊ��40����10��20��
��AB=BC=30��
��x��ʱ��C��B�ұ�ʱ��ǡ������MB=3BN��
��BM=![]() ��8x+4x+30����BN=
��8x+4x+30����BN=![]() ��30��4x��2x����
��30��4x��2x����
����MB=3BNʱ��![]() ��8x+4x+30��=3��
��8x+4x+30��=3��![]() ��30��4x��2x����
��30��4x��2x����
��ã�x=2��
��2��ʱǡ������MB=3BN��
��3����P��ʾ����Ϊ20��t����Q��ʾ����Ϊ20��3��t��30����
������P�ƶ�18��ʱ����Qû������ʱ��PQ�����ľ���ǡΪ18����λ��
����Q�ڵ�P���Ҳ࣬��20��3��t��30������20��t��=18��
���t=36��
������Q�ڵ�P����࣬��20��t��[20��3��t��30��]=18��
���t=54��
������������tΪ18�롢36���54��ʱ��P��Q�������18����λ���ȣ�


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
��ѧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD���ĸ��������������ϣ���A������Ϊ����3��0���������мף�����������ֱ��ɵ�Aͬʱ��������������ABCD�ı��������˶�������װ�˳ʱ�뷽�������˶��������Ұ���ʱ�뷽�������˶����������12���ӿɻ���һ�ܻص���A��������24���ӿɻ���һ�ܻص���A�������������˶���ĵ�2017�������ص�������� �� 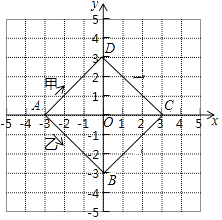
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧѧ����Ϊ�˽��Уѧ��ϲ���������������ȡ��������ķ�����������ƹ��������������ĸ����������������ѧ������Ȥ���ã���������Ľ�����Ƴ����µ�������������ͳ��ͼ����Ҫ��ÿλͬѧֻ��ѡ��һ���Լ�ϲ�������ࣻ����ͳ��ͼ����ƹ�������������������ϲ�������������е�ijһ�������ѧ���������������ͼ���ṩ����Ϣ������������⣺
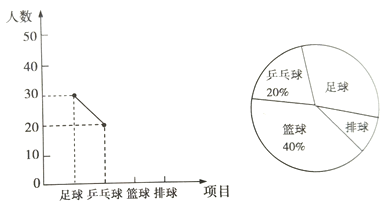
��1��������о��У�һ�������˶�����ѧ����
��2��ϲ�����������������ͳ��ͼ������Ӧ�����ε�Բ�Ľ��Ƕ��ٶȣ�
��3����ȫƵ���ֲ�����ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һƽ���ı���ABCD��һ������CEFG������E����AD�ϣ�����ECD=35�㣬��AEF=15�㣬���B�Ķ���Ϊ�Σ��������� 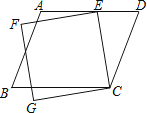
A.50
B.55
C.70
D.75
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AOD=150�㣬OB��OC��OM��ON �ǡ�AOD �ڵ����ߣ�����BOC=20�㣬��AOB=10�㣬OM ƽ�֡�AOC��ON ƽ�֡�BOD������BOC �ڡ�AOD �����ŵ� O�� 3��/����ٶ���ʱ����ת t ��ʱ������AOM����DON=3��4 ʱ���� t=____________��
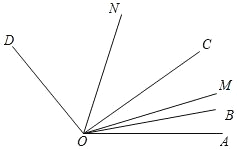
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������ɼ�����С��ͬ��С�������ɣ������������۲��� �������壬��������״��һ������ͼ��ʾ����
��1����������������ж��ٸ�С�����飬����ж��ٸ�С�����飻
��2�����ڷŵ�С���������ʱ���뻭��������۲쵽����ͼ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���� ![]() Ϊһ����ֱ��ϸ�ߣ�A��B������
Ϊһ����ֱ��ϸ�ߣ�A��B������ ![]() �ϣ���
�ϣ��� ![]() ��
�� ![]() =1��3��
=1��3�� ![]() ��
�� ![]() =3��5�����ȹ̶�B�㣬��
=3��5�����ȹ̶�B�㣬�� ![]() ����
���� ![]() ��ʹ��
��ʹ�� ![]() �ص���
�ص��� ![]() �ϣ���ͼ���������ٴ�ͼ������ ��A�㼰��A���ص���һ�������ʹ��ϸ�߷ֳ����Σ��������ϸ����С����ij��ȱ�Ϊ�Σ�������
�ϣ���ͼ���������ٴ�ͼ������ ��A�㼰��A���ص���һ�������ʹ��ϸ�߷ֳ����Σ��������ϸ����С����ij��ȱ�Ϊ�Σ������� 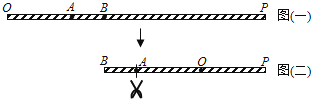
A.1��1��1
B.1��1��2
C.1��2��2
D.1��2��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ���ͬ�IJ�Ϊ����������ij��������������.
�磺2��2��2��(-3)��(-3)��(-3 )��( -3)��. ����������ij˷������ǰ� 2��2��2 ���� 2����������2 ��Ȧ 3 �η���. (-3)��(-3)��(-3 )��( -3)����(-3)����������-3 ��Ȧ 4 �η���.
һ��أ���![]() ��a��0������
��a��0������![]() ��������a��Ȧn�η���.
��������a��Ȧn�η���.
(1)ֱ��д���������� ![]() _____��
_____�� ![]() _________��
_________�� ![]() ___________��
___________��
(2)����֪�����������ļ����������ת��Ϊ�ӷ������������������ת��Ϊ�˷�������
�볢�Խ��������ij�������ת��Ϊ�˷�����������������һ��������������Ȧ n �η�����_____.
(3)���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��F��C��E��ֱ��l����F��C֮�䲻��ֱ�Ӳ���������A��D��l��࣬���AB=DE��AC=DF��BF=EC.

��1����֤����ABC�ա�DEF��
��2��ָ��ͼ������ƽ�е��߶Σ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com