
【题目】如图,在平面直角坐标系中,长方形纸片的AB边在y轴上,BC边在x轴上,B与坐标原点重合,折叠长方形ABCD的一边AD,使点D落在BC边的F处,折痕为AE,已知A点坐标为(0,8),C点坐标为(10,0). 求:E点坐标.
【答案】解:∵四边形ABCD为矩形,点B与点O重合, ∴DC=AB=8cm,AF=AD=BC=10.
设EF=DE=xcm,EC=8﹣x;
由勾股定理得:BF2=102﹣82 ,
∴BF=6,
∴CF=10﹣6=4;
在Rt△EFC中,由勾股定理得:x2=42+(8﹣x)2 ,
解得:x=5,
EC=8﹣5=3.
∴E点的坐标为(10,3).
【解析】根据勾股定理求出BF的长;进而求出FC的长度;由题意得EF=DE;利用勾股定理列出关于EC的方程,解方程即可解决问题.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】四边形ABCD 中,AB=3,BC=4,E,F 是对角线 AC上的两个动点,分别从 A,C 同时出发, 相向而行,速度均为 1cm/s,运动时间为 t 秒,当其中一个动点到达后就停止运动.
(Ⅰ)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 始终是平行四边形.
(Ⅱ)在(1)条件下,当 t 为何值时,四边形 EGFH 为矩形.
(Ⅲ)若 G,H 分别是折线 A﹣B﹣C,C﹣D﹣A 上的动点,与 E,F 相同的速度同时出发,当 t 为何值时,四边形 EGFH 为菱形.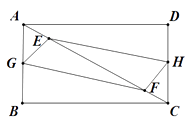
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10正方形网格中,每个小正方形的边长均为1个单位长度.点B、C坐标分别为(﹣4,2)、(﹣1,2).
(1)在图中建立平面直角坐标系,写出点A的坐标;
(2)将△ABC先向下平移4个单位,再向右平移5个单位得到△A1B1C1 , 画出△A1B1C1 , 并写出点C1的坐标;
(3)M(a,b)是△ABC内的一点,△ABC经过某种变换后点M的对应点为M2(a+1,b﹣7),画出△A2B2C2 . 并求出△A2B2C2的面积.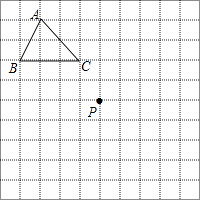
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2 . 
(1)用x表示花圃的一边BC的长,判断x=1是否符合题意,并说明理由;
(2)求y与x之间的关系式;
根据关系式补充表格:
x(米) | … | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | … |
y(米2) | … | 13.5 | 16 | 17.5 | 17.5 | 13.5 | … |
观察表中数据,写出y随x变化的一个特征: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,我国大约有1.3亿高血压病患者,占15岁以上总人口数的10%﹣15%,预防高血压不容忽视。“千帕kpa”和“毫米汞柱mmHg”都是表示血压的单位,前者是法定的国际计量单位,而后者则是过去一直广泛使用的惯用单位。请你根据下表所提供的信息,判断下列各组换算不正确的是( )
千帕kpa | 10 | 12 | 16 | … |
毫米汞柱mmHg | 75 | 90 | 120 | … |
A. 18kpa=135mmHg B. 21kpa=150mmHg C. 8kpa=60mmHg D. 32kpa=240mmHg
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com