
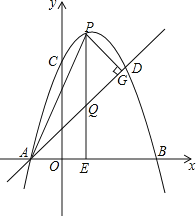
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),C(0,3)两点,点B是抛物线与x轴的另一个交点,点D与点C关于抛物线对称轴对称,作直线AD.点P在抛物线上,过点P作PE⊥x轴,垂足为点E,交直线AD于点Q,过点P作PG⊥AD,垂足为点G,连接AP.设点P的横坐标为m,PQ的长度为d.
(1)求抛物线的解析式;
(2)求点D的坐标及直线AD的解析式;
(3)当点P在直线AD上方时,求d关于m的函数关系式,并求出d的最大值;
(4)当点P在直线AD上方时,若PQ将△APG分成面积相等的两部分,直接写出m的值.
【答案】(1)y=﹣x2+2x+3;(2)点D的坐标为(2,3),直线AD的解析式为y=x+1;(3)d关于m函数关系式是d=﹣m2+m+2,d的最大值为![]() ;(4)m的值为0
;(4)m的值为0
【解析】
(1)根据待定系数法可求抛物线的解析式;
(2)将y=﹣x2+2x+3配方得抛物线的对称轴,根据轴对称的性质可得点D的坐标,再根据待定系数法可求直线AD的解析式;
(3)根据两点间的距离公式可得d=﹣m2+2m+3﹣m﹣1=﹣m2+m+2=﹣(m﹣![]() )2+
)2+![]() ,依此可求d的最大值;
,依此可求d的最大值;
(4)可设直线PG的解析式为y=﹣x+p,根据中点坐标公式可得G的坐标,再根据待定系数法可求m的值.
解:(1)∵抛物线y=﹣x2+bx+c 经过A(﹣1,0),C(0,3)两点,
∴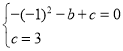 ,
,
解得![]() .
.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)∵将y=﹣x2+2x+3配方,得y=﹣(x﹣1)2+4,
∴抛物线的对称轴是直线x=1.
∴点D的坐标为(2,3).
设直线AD的解析式为y=kx+n,
由题意,得![]() ,
,
解得![]() .
.
∴直线AD的解析式为y=x+1.
(3)∵点P的横坐标为m,
∴点P,Q的纵坐标分别为﹣m2+2m+3,m+1,
∴d=﹣m2+2m+3﹣m﹣1=﹣m2+m+2=![]() ,
,
∴d关于m函数关系式是d=﹣m2+m+2,d的最大值为![]() .
.
(4)设直线PG的解析式为y=﹣x+p,
∵PQ将△APG分成面积相等的两部分,
∴G的坐标为(2m+1,2m+2),
∴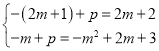 ,
,
解得m1=0,m2=﹣1(不合题意舍去).
故m的值为0.


科目:初中数学 来源: 题型:
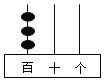
【题目】把3颗算珠放在计数器的3根插棒上构成一个数字,例如,如图摆放的算珠表示数300.现将3颗算珠任意摆放在这3根插棒上.
(1)若构成的数是两位数,则十位数字为1的概率为 ;
(2)求构成的数是三位数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
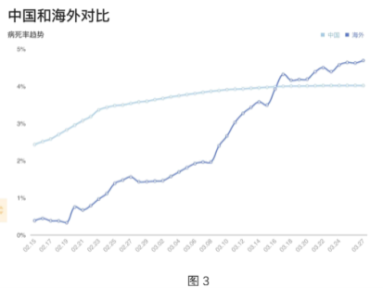
【题目】图1是2020年3月26日全国新冠疫情数据表,图2是3月28日海外各国疫情统计表,图3是中国和海外的病死率趋势对比图,根据这些图表,选出下列说法中错误的一项( )


A.图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量.
B.图2显示美国累计确诊人数虽然约是德国的两倍,但每百万人口的确诊人数大约只有德国的一半.
C.图2显示意大利当前的治愈率高于西班牙.
D.图3显示大约从3月16日开始海外的病死率开始高于中国的病死率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年9月9日兰州市秦王川国家湿地公园在万众瞩目中盛大开园,公园被分为六大板块,分别为:亲水运动公园、西北戴维营、私人农场区、湿地生态培育区、丝路古镇、湿地科普活动区(分别记为A,B,C,D,E,F),为了了解游客“最喜欢板块”的情况,随机对部分游客进行问卷调查,规定每个人从这六个板块中选择一个,并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息回答下列问题:
(1)这次调查的样本容量是 ,a= ;
(2)扇形统计图中“C”对应的圆心角为 ;
(3)补全条形统计图;
(4)若2019年预计有100000人进园游玩,请估计最喜欢板块为“B”的游客人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的半径为 4,
的半径为 4,![]() 是圆的直径,点
是圆的直径,点![]() 是
是![]() 的切线
的切线![]() 上的一个动点,连接
上的一个动点,连接![]() 交
交![]() 于点
于点![]() ,弦
,弦![]() 平行于
平行于![]() ,连接
,连接![]() .
.
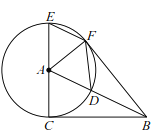
(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() __________时,四边形
__________时,四边形![]() 为菱形;
为菱形;
(3)当![]() ___________时,四边形
___________时,四边形![]() 为正方形.
为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
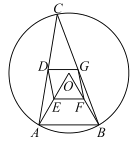
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E.

(1)求证:AC是⊙O的切线;
(2)若AD∶DB=3∶2,AC=15,求⊙O的直径;
(3)在(2)的条件下,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
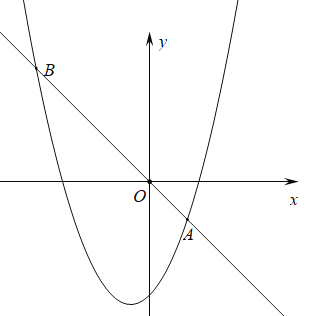
【题目】已知抛物线![]() 经过点
经过点![]() ,
,![]() .把抛物线
.把抛物线![]() 与线段
与线段![]() 围成的封闭图形记作
围成的封闭图形记作![]() .
.
(1)求此抛物线的解析式;
(2)点![]() 为图形
为图形![]() 中的抛物线上一点,且点
中的抛物线上一点,且点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴,交线段
轴,交线段![]() 于点
于点![]() .当
.当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]() 的值;
的值;
(3)点![]() 是直线
是直线![]() 上一点,且点
上一点,且点![]() 的横坐标为
的横坐标为![]() ,以线段
,以线段![]() 为边作正方形
为边作正方形![]() ,且使正方形
,且使正方形![]() 与图形
与图形![]() 在直线
在直线![]() 的同侧,当
的同侧,当![]() ,
,![]() 两点中只有一个点在图形
两点中只有一个点在图形![]() 的内部时,请直接写出
的内部时,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com