
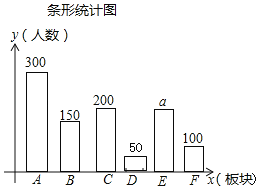
ЁОЬтФПЁП2018Фъ9дТ9ШеРМжнЪаЧиЭѕДЈЙњМвЪЊЕиЙЋдАдкЭђжкжѕФПжаЪЂДѓПЊдАЃЌЙЋдАБЛЗжЮЊСљДѓАхПщЃЌЗжБ№ЮЊЃКЧзЫЎдЫЖЏЙЋдАЁЂЮїББДїЮЌгЊЁЂЫНШЫХЉГЁЧјЁЂЪЊЕиЩњЬЌХрг§ЧјЁЂЫПТЗЙХеђЁЂЪЊЕиПЦЦеЛюЖЏЧјЃЈЗжБ№МЧЮЊAЃЌBЃЌCЃЌDЃЌEЃЌFЃЉЃЌЮЊСЫСЫНтгЮПЭЁАзюЯВЛЖАхПщЁБЕФЧщПіЃЌЫцЛњЖдВПЗжгЮПЭНјааЮЪОэЕїВщЃЌЙцЖЈУПИіШЫДгетСљИіАхПщжабЁдёвЛИіЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ИљОнвдЩЯаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉетДЮЕїВщЕФбљБОШнСПЪЧЁЁ ЁЁЃЌaЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЁАCЁБЖдгІЕФдВаФНЧЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ4ЃЉШє2019ФъдЄМЦга100000ШЫНјдАгЮЭцЃЌЧыЙРМЦзюЯВЛЖАхПщЮЊЁАBЁБЕФгЮПЭШЫЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ1000ЃЌ200ЃЛЃЈ2ЃЉ72ЁуЃЛЃЈ3ЃЉМћНтЮіЃЛЃЈ4ЃЉзюЯВЛЖАхПщЮЊЁАBЁБЕФгЮПЭШЫЪ§ЮЊ15000ШЫЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЕїВщЕФбљБОШнСПЃК300ЁТ30%ЃН1000ЃЈШЫЃЉЃЌЫПТЗЙХеђЕФШЫЪ§ЃК3000ЁС20%ЃН200ЃЈШЫЃЉЃЌ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЁАCЁБЖдгІЕФдВаФНЧЃК![]() ЃН72ЁуЃЌ
ЃН72ЁуЃЌ
ЃЈ3ЃЉDЕФШЫЪ§ЃК1000Љ300Љ150Љ200Љ200Љ100ЃН50ЃЈШЫЃЉЃЌОнДЫВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ4ЃЉзюЯВЛЖАхПщЮЊЁАBЁБЕФгЮПЭШЫЪ§ЃК100000ЁС![]() ЃН15000ЃЈШЫЃЉЃЎ
ЃН15000ЃЈШЫЃЉЃЎ
НтЃКЃЈ1ЃЉЕїВщЕФбљБОШнСПЃК300ЁТ30%ЃН1000ЃЈШЫЃЉЃЌ
ЫПТЗЙХеђЕФШЫЪ§ЃК3000ЁС20%ЃН200ЃЈШЫЃЉЃЌ
ЙЪД№АИЮЊ1000ЃЌ200ЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЁАCЁБЖдгІЕФдВаФНЧЃК![]() ЃН72ЁуЃЌ
ЃН72ЁуЃЌ
ЙЪД№АИЮЊ72ЁуЃЛ
ЃЈ3ЃЉDЕФШЫЪ§ЃК1000Љ300Љ150Љ200Љ200Љ100ЃН50ЃЈШЫЃЉЃЌ
ВЙШЋЬѕаЮЭГМЦЭМШчЯТЃК
ЃЈ4ЃЉзюЯВЛЖАхПщЮЊЁАBЁБЕФгЮПЭШЫЪ§ЃК100000ЁС![]() ЃН15000ЃЈШЫЃЉЃЌ
ЃН15000ЃЈШЫЃЉЃЌ
Д№ЃКзюЯВЛЖАхПщЮЊЁАBЁБЕФгЮПЭШЫЪ§ЮЊ15000ШЫЃЎ


 вЛПЮвЛСЗвЛБОЭЈЯЕСаД№АИ
вЛПЮвЛСЗвЛБОЭЈЯЕСаД№АИ еуНжЎаЧбЇвЕЫЎЦНВтЪдЯЕСаД№АИ
еуНжЎаЧбЇвЕЫЎЦНВтЪдЯЕСаД№АИ ИпаЇжЧФмПЮЪБзївЕЯЕСаД№АИ
ИпаЇжЧФмПЮЪБзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЁЂCЁЂFдкзјБъжсЩЯЃЌEЪЧOAЕФжаЕуЃЌЫФБпаЮAOCBЪЧОиаЮЃЌЫФБпаЮBDEFЪЧе§ЗНаЮЃЌШєЕуCЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌдђЕуDЕФзјБъЮЊЃЈЁЁЁЁЃЉ
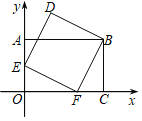
A. ЃЈ1ЃЌ2.5ЃЉB. ЃЈ1ЃЌ1+ ![]() ЃЉC. ЃЈ1ЃЌ3ЃЉD. ЃЈ
ЃЉC. ЃЈ1ЃЌ3ЃЉD. ЃЈ![]() Љ1ЃЌ1+
Љ1ЃЌ1+ ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊТњзуЪаГЁашЧѓЃЌаТЩњЛюГЌЪадкЖЫЮчНкЧАЯІЙКНјМлИёЮЊ3дЊ/ИіЕФФГЦЗХЦєезгЃЌИљОнЪаГЁдЄВтЃЌИУЦЗХЦєезгУПИіЪлМл4дЊЪБЃЌУПЬьФмГіЪл500ИіЃЌВЂЧвЪлМлУПЩЯеЧ0.1дЊЃЌЦфЯњЪлСПНЋМѕЩй10ИіЃЌЮЊСЫЮЌЛЄЯћЗбепРћвцЃЌЮяМлВПУХЙцЖЈЃЌИУЦЗХЦєезгЪлМлВЛФмГЌЙ§НјМлЕФ200%ЃЌЧыФуРћгУЫљбЇжЊЪЖАяжњГЌЪаИјИУЦЗХЦєезгЖЈМлЃЌЪЙГЌЪаУПЬьЕФЯњЪлРћШѓЮЊ800дЊЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧБп
ЪЧБп![]() ЕФжаЕуЃЌЙ§Еу
ЕФжаЕуЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЕФЭтНгдВгыБп
ЕФЭтНгдВгыБп![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЃЈ1ЃЉЂйВЙШЋЭМаЮЃЛЂкХаЖЯжБЯп![]() гы
гы![]() ЕФЭтНгдВЕФЙЋЙВЕуИіЪ§ЃЌВЂИјГіжЄУїЃЎ
ЕФЭтНгдВЕФЙЋЙВЕуИіЪ§ЃЌВЂИјГіжЄУїЃЎ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
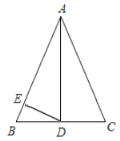
ЁОЬтФПЁПЯТУцЪЧаЁЛЊЩшМЦЕФЁАзївЛИіНЧЕШгквбжЊНЧЕФ2БЖЁБЕФГпЙцзїЭМЙ§ГЬЃЎ
вбжЊЃК![]() ЃЎ
ЃЎ
ЧѓзїЃК![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЎ
ЃЎ
зїЗЈЃКШчЭМЃЌ
ЂйдкЩфЯп![]() ЩЯШЮШЁвЛЕу
ЩЯШЮШЁвЛЕу![]() ЃЛ
ЃЛ
ЂкзїЯпЖЮ![]() ЕФДЙжБЦНЗжЯпЃЌНЛ
ЕФДЙжБЦНЗжЯпЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЛ
ЃЛ
ЂлСЌНг![]() ЃЛ
ЃЛ
Ыљвд![]() МДЮЊЫљЧѓзїЕФНЧЃЎ
МДЮЊЫљЧѓзїЕФНЧЃЎ
ИљОнаЁЛЊЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
(1)ЪЙгУжБГпКЭдВЙцВЙШЋЭМаЮ(БЃСєзїЭМКлМЃ)ЃЛ
(2)ЭъГЩЯТУцЕФжЄУї(ЫЕУїЃКРЈКХРяЬюаДЭЦРэЕФвРОн)ЃЎ
жЄУїЃКЁп![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФДЙжБЦНЗжЯпЃЌ
ЕФДЙжБЦНЗжЯпЃЌ
Ёр![]() ______(______)
______(______)
Ёр![]() ЃЎ
ЃЎ
Ёп![]() (______)
(______)
Ёр![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
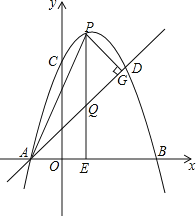
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНЉx2+bx+cОЙ§A(Љ1ЃЌ0)ЃЌC(0ЃЌ3)СНЕуЃЌЕуBЪЧХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЃЌЕуDгыЕуCЙигкХзЮяЯпЖдГЦжсЖдГЦЃЌзїжБЯпADЃЎЕуPдкХзЮяЯпЩЯЃЌЙ§ЕуPзїPEЁЭxжсЃЌДЙзуЮЊЕуEЃЌНЛжБЯпADгкЕуQЃЌЙ§ЕуPзїPGЁЭADЃЌДЙзуЮЊЕуGЃЌСЌНгAPЃЎЩшЕуPЕФКсзјБъЮЊmЃЌPQЕФГЄЖШЮЊdЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)ЧѓЕуDЕФзјБъМАжБЯпADЕФНтЮіЪНЃЛ
(3)ЕБЕуPдкжБЯпADЩЯЗНЪБЃЌЧѓdЙигкmЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіdЕФзюДѓжЕЃЛ
(4)ЕБЕуPдкжБЯпADЩЯЗНЪБЃЌШєPQНЋЁїAPGЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃЌжБНгаДГіmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
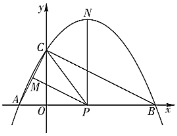
ЁОЬтФПЁПШчЭМ1ЃЌОЙ§дЕуOЕФХзЮяЯп![]() ЃЈaЁй0ЃЉгыxжсНЛгкСэвЛЕуAЃЈ
ЃЈaЁй0ЃЉгыxжсНЛгкСэвЛЕуAЃЈ![]() ЃЌ0ЃЉЃЌдкЕквЛЯѓЯоФкгыжБЯпy=xНЛгкЕуBЃЈ2ЃЌtЃЉЃЎ
ЃЌ0ЃЉЃЌдкЕквЛЯѓЯоФкгыжБЯпy=xНЛгкЕуBЃЈ2ЃЌtЃЉЃЎ
ЃЈ1ЃЉЧѓетЬѕХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкЕкЫФЯѓЯоФкЕФХзЮяЯпЩЯгавЛЕуCЃЌТњзувдBЃЌOЃЌCЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЮЊ2ЃЌЧѓЕуCЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуMдкетЬѕХзЮяЯпЩЯЃЌЧвЁЯMBO=ЁЯABOЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЪЧЗёДцдкЕуPЃЌЪЙЕУЁїPOCЁзЁїMOBЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§![]()
![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЕуЃЌ
ЩЯвЛЕуЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() жсНЛХзЮяЯпгкЕу
жсНЛХзЮяЯпгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЂйЕБ![]() ЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЕу
ЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкЧѓ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉжБНгаДГіЕБ![]() УцЛ§зюДѓЪБЃЌЕу
УцЛ§зюДѓЪБЃЌЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
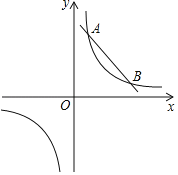
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНЉx+bгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМаЮНЛгкAЃЈaЃЌ4ЃЉКЭBЃЈ4ЃЌ1ЃЉСНЕу
ЕФЭМаЮНЛгкAЃЈaЃЌ4ЃЉКЭBЃЈ4ЃЌ1ЃЉСНЕу
ЃЈ1ЃЉЧѓbЃЌkЕФжЕЃЛ
ЃЈ2ЃЉШєЕуCЃЈxЃЌyЃЉвВдкЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌЧѓЕБ2ЁмxЁм6ЪБЃЌКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЛ
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌЧѓЕБ2ЁмxЁм6ЪБЃЌКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉНЋжБЯпyЃНЉx+bЯђЯТЦНвЦmИіЕЅЮЛЃЌЕБжБЯпгыЫЋЧњЯпУЛгаНЛЕуЪБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com