
【题目】如图,已知二次函数![]()
![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 轴交抛物线于点
轴交抛物线于点![]() .
.
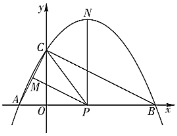
(1)求二次函数![]() 的解析式;
的解析式;
(2)①当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
②求![]() 的最大值;
的最大值;
(3)直接写出当![]() 面积最大时,点
面积最大时,点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①点
;(2)①点![]() 的坐标为
的坐标为![]() 或
或![]() ;②
;②![]() ;(3)
;(3)![]()
【解析】
(1)已知抛物线上点的坐标,用待定系数法即可得出抛物线解析式.
(2)①已知B、C点坐标,求出BC,根据等腰三角形性质,当时![]() ,即可求出点P坐标;当
,即可求出点P坐标;当![]() 时,过点
时,过点![]() 作
作![]() .设
.设![]() ,则
,则![]() ,根据勾股定理求出t,即可求出P点坐标.
,根据勾股定理求出t,即可求出P点坐标.
②已知抛物线解析式,可求得A点坐标,根据勾股定理可验证![]() 是直角三角形.设点
是直角三角形.设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,由
,由![]() ,可将PM和PN用t表示出来,
,可将PM和PN用t表示出来,![]() 是关于t的二次函数,根据二次函数性质可求出最大值.
是关于t的二次函数,根据二次函数性质可求出最大值.
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]()
证明△AMP∽△ACB,![]() ,得出
,得出![]() ,
,![]() ,得出关于t的一元二次方程,根据函数性质,得出当t=3时,面积有最大值,再求出P点坐标.
,得出关于t的一元二次方程,根据函数性质,得出当t=3时,面积有最大值,再求出P点坐标.
解:(1)二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
∴![]()
解得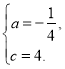
∴抛物线的解析式为![]() .
.
故答案为:![]()
(2)①∵![]() ,
,![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() .
.
∴点![]() 的坐标为
的坐标为![]() ;
;
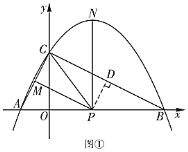
当![]() 时,如图①,过点
时,如图①,过点![]() 作
作![]() .设
.设![]() ,则
,则![]() .
.
∴![]() .解得
.解得![]() .
.
此时点![]() 的坐标为
的坐标为![]() .
.
综上,当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
②令![]() ,则
,则![]() .
.
解得![]() ,
,![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
∴![]() ,
,![]() .又
.又![]() ,
,
∴![]() 是直角三角形.
是直角三角形.
∵![]() ,
,
∴![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() 的最大值为
的最大值为![]() .
.
故答案为:![]() 或
或![]() ;
;![]()
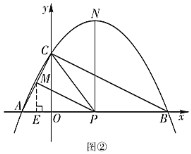
(3)如图②,过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]()
∵PM∥BCM,∠APM=∠ABC
∴ △AMP∽△ACB
∴![]()
∴![]()
∴![]() .
.
∵![]() ∴当
∴当![]() 时,
时,![]() 的最大面积是5.
的最大面积是5.
∴点![]() 的坐标为
的坐标为![]() .
.
故答案为:P![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在不是菱形的平行四边形![]() 中,
中,![]() 在对角线
在对角线![]() 上,在以下三个条件中再选一个,①
上,在以下三个条件中再选一个,①![]() 分别是
分别是![]() 的中线,②
的中线,②![]() 分别是
分别是![]() 的角平分线,③
的角平分线,③![]() .使得四边形
.使得四边形![]() 是平行四边形,并说明理由.
是平行四边形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年9月9日兰州市秦王川国家湿地公园在万众瞩目中盛大开园,公园被分为六大板块,分别为:亲水运动公园、西北戴维营、私人农场区、湿地生态培育区、丝路古镇、湿地科普活动区(分别记为A,B,C,D,E,F),为了了解游客“最喜欢板块”的情况,随机对部分游客进行问卷调查,规定每个人从这六个板块中选择一个,并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息回答下列问题:
(1)这次调查的样本容量是 ,a= ;
(2)扇形统计图中“C”对应的圆心角为 ;
(3)补全条形统计图;
(4)若2019年预计有100000人进园游玩,请估计最喜欢板块为“B”的游客人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
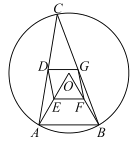
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )经过点
)经过点![]() 和
和![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() 随着
随着![]() 的增大而减小.下列结论:①
的增大而减小.下列结论:①![]() ;②若点
;②若点![]() ,点
,点![]() 都在抛物线上,则
都在抛物线上,则![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E.

(1)求证:AC是⊙O的切线;
(2)若AD∶DB=3∶2,AC=15,求⊙O的直径;
(3)在(2)的条件下,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,CD为⊙O的切线,C为切点,过A作CD的垂线,垂足为D.
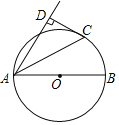
(1)求证:AC平分∠BAD;
(2)若⊙O半径为5,CD=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点A,它的顶点为点B.
与y轴交于点A,它的顶点为点B.
(1)点A的坐标为______,点B的坐标为______(用m表示);
(2)已知点M(-6,4),点N(3,4),若抛物线与线段MN恰有一个公共点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com