
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点A,它的顶点为点B.
与y轴交于点A,它的顶点为点B.
(1)点A的坐标为______,点B的坐标为______(用m表示);
(2)已知点M(-6,4),点N(3,4),若抛物线与线段MN恰有一个公共点,结合函数图象,求m的取值范围.
【答案】(1)(0,1),(m,1-m);(2)当m<-4,或m=-3或m>1时,抛物线与线段MN恰好有一个公共点
【解析】
(1)根据计算x=0即可得到点A的坐标,利用顶点坐标公式计算顶点坐标;
(2)根据题意画出函数图象,利用分类讨论的方法即可得到m的取值范围.
(1)当x=0时,得到y=1,∴点A的坐标是(0,1),
∵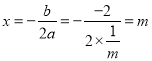 ,
, 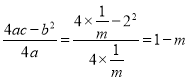 ,
,
∴顶点B的坐标是(m,1-m),
故答案为:(0,1),(m,1-m);
(2)①当m<0时,
如图1:当m=-4时,抛物线与线段MN有两个公共点,且此时点M恰好在抛物线上,
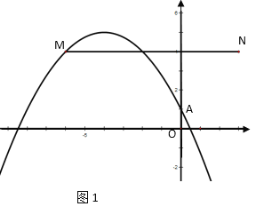
如图2:当m<-4时,此时点M在抛物线内,点N在抛物线外,抛物线与线段MN有一个交点,
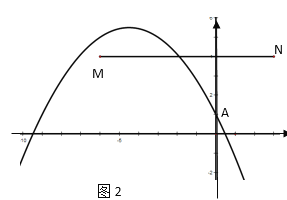
当-4<m<-3时,如图3,抛物线与线段MN有两个交点,
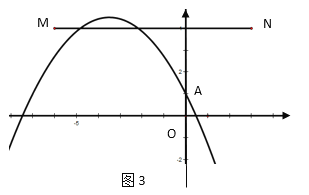
当m=-3时,如图4,抛物线与线段MN有一个交点,
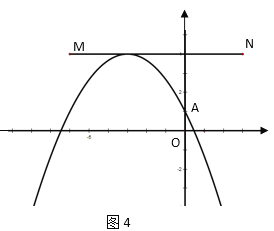
当-3<m<0时,抛物线与线段MN没有交点,
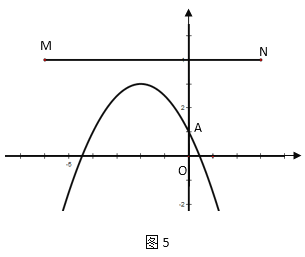
②当m>0时,
当0<m![]() 时,抛物线与线段MN有两个交点,
时,抛物线与线段MN有两个交点,
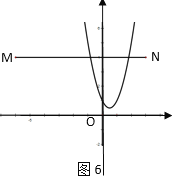
当m>1时,如图7,物线与线段MN有一个交点,
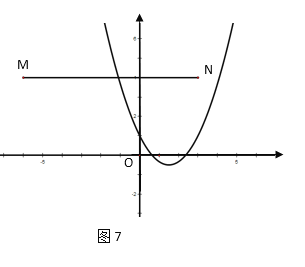
综上,当m<-4,或m=-3或m>1时,抛物线与线段MN恰好有一个公共点


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
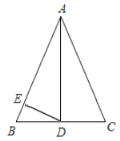
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 的外接圆与边
的外接圆与边![]() 交于点
交于点![]() ,
,![]() ,
,
(1)①补全图形;②判断直线![]() 与
与![]() 的外接圆的公共点个数,并给出证明.
的外接圆的公共点个数,并给出证明.
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]()
![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 轴交抛物线于点
轴交抛物线于点![]() .
.
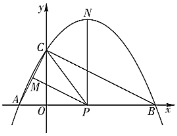
(1)求二次函数![]() 的解析式;
的解析式;
(2)①当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
②求![]() 的最大值;
的最大值;
(3)直接写出当![]() 面积最大时,点
面积最大时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )
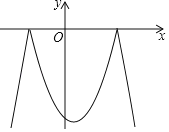
A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
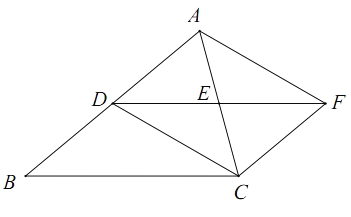
【题目】如图,在△ABC中,D为AB中点,过点D作DF//BC交AC于点E,且DE=EF,连接AF,CF,CD.
(1)求证:四边形ADCF为平行四边形;
(2)若∠ACD=45°,∠EDC=30°,BC=4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°(AC>BC),用尺规作图的方法作线段AD,保留作图痕迹如图所示,认真观察作图痕迹,若CD=4,BD=5,则AC的长为( )
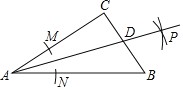
A.6B.9C.12D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
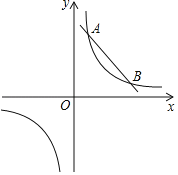
【题目】如图,直线y=﹣x+b与反比例函数y=![]() 的图形交于A(a,4)和B(4,1)两点
的图形交于A(a,4)和B(4,1)两点
(1)求b,k的值;
(2)若点C(x,y)也在反比例函数y=![]() (x>0)的图象上,求当2≤x≤6时,函数值y的取值范围;
(x>0)的图象上,求当2≤x≤6时,函数值y的取值范围;
(3)将直线y=﹣x+b向下平移m个单位,当直线与双曲线没有交点时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
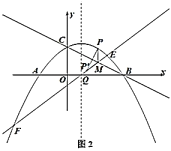
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点
轴交点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .如图1,点
.如图1,点![]() 为抛物线上任意一点,过点
为抛物线上任意一点,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() .
.
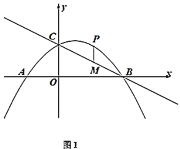
(1)求抛物线的解析式;
(2)当![]() 是直角三角形时,求
是直角三角形时,求![]() 点坐标;
点坐标;
(3)如图2,作![]() 点关于直线
点关于直线![]() 的对称点
的对称点![]() ,作直线
,作直线![]() 与抛物线交于
与抛物线交于![]() ,设抛物线对称轴与
,设抛物线对称轴与![]() 轴交点为
轴交点为![]() ,当直线
,当直线![]() 经过点
经过点![]() 时,请你直接写出
时,请你直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
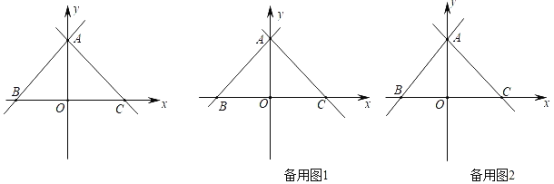
【题目】如图,在平面直角坐标系,点O是原点,直线y=x+6分别交x轴,y轴于点B,A,经过点A的直线y=﹣x+b交x轴于点 C.
(1)求b的值;
(2)点D是线段AB上的一个动点,连接OD,过点O作OE⊥OD交AC于点E,连接DE,将△ODE沿DE折叠得到△FDE,连接AF.设点D的横坐标为t,AF的长为d,当t>﹣3时,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,DE交OA于点G,且tan∠AGD=3.点H在x轴上(点H在点O的右侧),连接DH,EH,FH,当∠DHF=∠EHF时,请直接写出点H的坐标,不需要写出解题过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com