
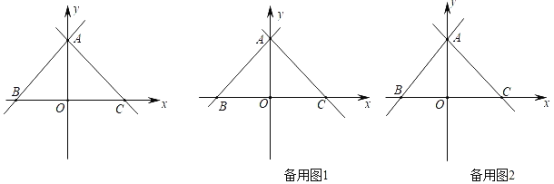
【题目】如图,在平面直角坐标系,点O是原点,直线y=x+6分别交x轴,y轴于点B,A,经过点A的直线y=﹣x+b交x轴于点 C.
(1)求b的值;
(2)点D是线段AB上的一个动点,连接OD,过点O作OE⊥OD交AC于点E,连接DE,将△ODE沿DE折叠得到△FDE,连接AF.设点D的横坐标为t,AF的长为d,当t>﹣3时,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,DE交OA于点G,且tan∠AGD=3.点H在x轴上(点H在点O的右侧),连接DH,EH,FH,当∠DHF=∠EHF时,请直接写出点H的坐标,不需要写出解题过程.
【答案】(1)6;(2)d=6+2t;(3)H点的坐标为H1(10,0),H2(2,0).
【解析】
(1)由y=x+6求得A点坐标,再将A点坐标代入y=﹣x+b中,便可求得b;
(2)过点D分别作DM⊥x轴于点M,DN⊥y轴于点N,过点F作FR⊥AF交AE于点R,可证明四边形ODFE为正方形,再△AOD≌△COE(ASA),用t表示AD,再△ADF≌△REF(AAS),进而用t表示AR,问题便可迎刃而解;
(3)分两种情况解答:第一种情况,当FH平分∠DHE时,连接OF,过E作EK⊥x轴于点K,用EL⊥y轴于点L,设正方形ODFE的外接圆交x轴于点H,证明△ODM≌△EOK(AAS),用t表示出EL,OL,再由tan∠AGD=3,便可用t表示GN,GL,由OA=6列出t的方程求得t,便可求得H点坐标;第二种情况,当∠DHF与∠EHF重合时,延长DE与x轴交于点H,求出DE与x轴的交点坐标便可.
解:(1)令x=0,得y=x+6=6,
∴A(0,6),
把A(0,6)代入y=﹣x+b中,得b=6;
(2)令y=0,得y=x+6=0,则x=﹣6,
∴B(﹣6,0),
∵点D的横坐标为t,
∴D(t,t+6),
令y=0,得y=﹣x+6=0,x=6,
∴C(6,0),
∵OA=OB=6,
∴∠OAB=∠OBA=45°,
同理∠OAC=∠OCA=45°,
∴∠BAC=90°,
在Rt△AOC中,AC=![]() ,
,
过点D分别作DM⊥x轴于点M,DN⊥y轴于点N,
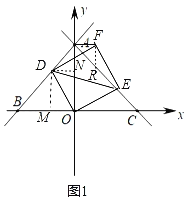
∵∠DMO=∠MON=∠OND=90°,
∴四边形DMON为矩形,
∴DN=OM=﹣t,
在Rt△ADN中,∠DAN=45°,AD=﹣![]() t,
t,
∵∠AOD+∠AOE=90°,∠COE+∠AOE=90°,
∴∠AOD=∠COE,
又∵∠OAD=∠OCE=45°,OA=OC,
∴△AOD≌△COE(ASA),
∴OD=OE,AD=CE=﹣![]() t,
t,
∵△DFE和△DOE关于DE对称,
∴DF=OD=0E=EF,∠DFE=∠DOE=90°,
过点F作FR⊥AF交AE于点R,
∵∠AFD+∠DFR=90°,∠RFE+∠DFR=90°,
∴∠AFD=∠RFE,
∵∠ERF=∠RAF+∠AFR=∠RAF+90°,
∠DAF=∠RAF+∠DAR=∠RAF+90°,
∴∠REF=∠DAF,
∴△ADF≌△REF(AAS),
∴AF=RF,AD=RE=![]() ,
,
∴∠FAR=∠FRA,
又∵∠FAR+∠FRA═90°,
∴∠FAR=∠FRA=45°,
在Rt△AFR中,AR=AC﹣CE﹣ER=6![]() +2
+2![]() t,
t,
AF=![]() ,
,
∴d=6+2t;
(3)连接OF,过E作EK⊥x轴于点K,用EL⊥y轴于点L,设正方形ODFE的外接圆交x轴于点H,

∴∠DOM+∠ODM=∠DOM+∠EOK=90°,
∴∠ODM=∠EOK,
∵∠OMD=∠EKO=90°,OD=EO,
∴△ODM≌△EOK(AAS),
∴EK=OM=DN=OL=﹣t,LE=OK=DM=6+t,
∵tan∠AGD=3.DN=﹣t,
∴![]() ,即
,即![]() ,
,
∴GN=![]() ,GL=
,GL=![]() ,
,
∴OA=OL+GL+GN+AN=﹣t+![]() ,
,
∵OA=6,
∴﹣2t+2=6,
∴t=﹣2,
∴AF=6+2t═2,
∵OF是正方形ODFE的外接圆的直径,
∴FH⊥x轴,∠DHF=∠DOF=∠EOF=45°=∠EHF
∴H(2,0),此时满足条件;
如图3,延长DE与x轴交于点H,则∠DHF=∠EHF,

由上知D(﹣2,4),E(4,2),
设直线DE的解析式为:y=kx+b(k≠0),则
![]() ,
,
∴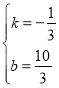 ,
,
∴直线DE的解析式为:![]() ,
,
当y=0时,得![]() ,
,
解得,x=10,
∴H(10,0),
综上,H点的坐标为H1(10,0),H2(2,0).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点A,它的顶点为点B.
与y轴交于点A,它的顶点为点B.
(1)点A的坐标为______,点B的坐标为______(用m表示);
(2)已知点M(-6,4),点N(3,4),若抛物线与线段MN恰有一个公共点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
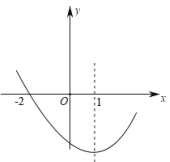
【题目】如图,二次函数![]() 的图象过点
的图象过点![]() ,对称轴为直
,对称轴为直![]() 线,下列结论中一定正确的是____________(填序号即可).
线,下列结论中一定正确的是____________(填序号即可).
①![]() ;
;
②若![]() 是抛物线上的两点,当
是抛物线上的两点,当![]() 时,
时,![]()
③若方程![]() 的两根为
的两根为![]() ,且
,且![]() ,则
,则![]()
④![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图 1、图 2 均是 6×6 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为 1,点 A、B、C、D 均在格点上.在图 1、图 2 中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
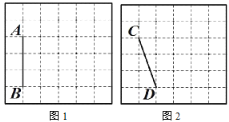
(1)在图 1 中以线段 AB 为边画一个△ABM,使∠ABM=45°,且△ABM 的面积为 6;
(2)在图 2 中以线段 CD 为边画一个四边形 CDEF,使∠CDE=∠CFE=90°,且四边形 CDEF 的面积为 8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() . 点
. 点![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点, 连接
重合的任意一点, 连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]()
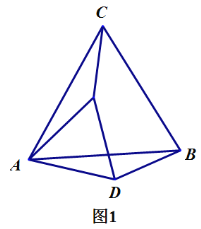
(1)动手操作
如图1,当![]() 时,我们通过用 刻度尺和量角器度量发现:
时,我们通过用 刻度尺和量角器度量发现:
![]() 的值是
的值是![]() ;直线
;直线![]() 与直线
与直线![]() 相交所成的较小角的度数是
相交所成的较小角的度数是![]() ;
;
请证明以上结论正确.
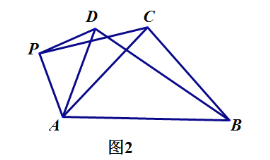
(2)类比探究
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并就图2的情形说明理由.
相交所成的较小角的度数,并就图2的情形说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
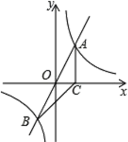
【题目】如图,正比例函数y=2x的图象与反比例函数y=![]() 的图象交于A,B两点,过点A作AC垂直x轴于点C,连接BC.若△ABC的面积为2.
的图象交于A,B两点,过点A作AC垂直x轴于点C,连接BC.若△ABC的面积为2.
(1)求k的值;
(2)直接写出![]() >2x时,自变量x的取值范围.
>2x时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接体育中考,某校九(1)班的体育老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,该班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
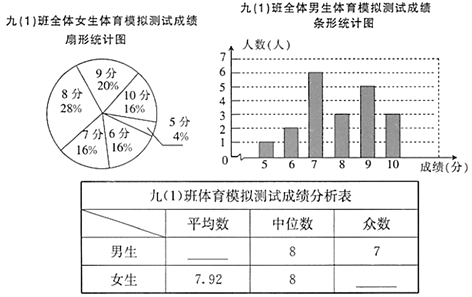
根据以上信息,解答下列问题.
(1)这个班共有男生_________人,女生有____________人.
(2)请你补全九(1)班体育模拟测试成绩分析表.
(3)你认为在这次体育模拟测试中,九(1)班的全体男生和全体女生,谁的表现更好一些?请写出一条支持你的看法的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com