
【题目】在![]() 中,
中,![]() . 点
. 点![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点, 连接
重合的任意一点, 连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]()
(1)动手操作
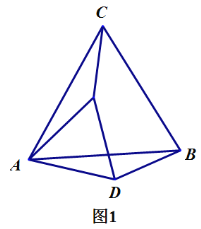
如图1,当![]() 时,我们通过用 刻度尺和量角器度量发现:
时,我们通过用 刻度尺和量角器度量发现:
![]() 的值是
的值是![]() ;直线
;直线![]() 与直线
与直线![]() 相交所成的较小角的度数是
相交所成的较小角的度数是![]() ;
;
请证明以上结论正确.
(2)类比探究
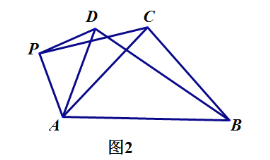
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并就图2的情形说明理由.
相交所成的较小角的度数,并就图2的情形说明理由.
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°(AC>BC),用尺规作图的方法作线段AD,保留作图痕迹如图所示,认真观察作图痕迹,若CD=4,BD=5,则AC的长为( )
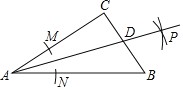
A.6B.9C.12D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,点C,D在⊙O上,![]() 连接AD,OC.
连接AD,OC.
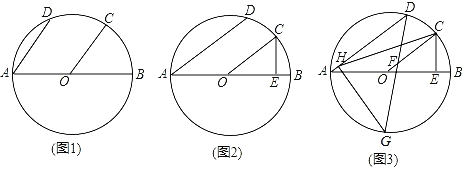
(1)如图1,求证:AD∥OC;
(2)如图2,过点C作CE⊥AB于点E,求证:AD=2OE;
(3)如图3,在(2)的条件下,点F在OC上,且OF=BE,连接DF并延长交⊙O于点G,过点G作CH⊥AD于点H,连接CH,若∠CFG=135°,CE=3,求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
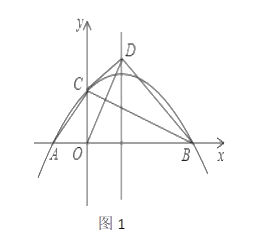
【题目】如图,在平面直角坐标系中,抛物线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 将
将![]() 沿
沿![]() 所在的直线翻折,得到
所在的直线翻折,得到![]() 连接
连接![]() .
.
(1)若![]() 求抛物线的解析式.
求抛物线的解析式.
(2)如图1,设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,![]() 若
若![]() 点是半径为
点是半径为![]() 的
的![]() 上一动点,连接
上一动点,连接![]() 当点
当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的值最大,请求出这个最大值,并说明理由.
的值最大,请求出这个最大值,并说明理由.
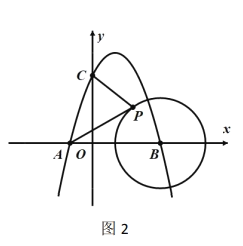
查看答案和解析>>
科目:初中数学 来源: 题型:
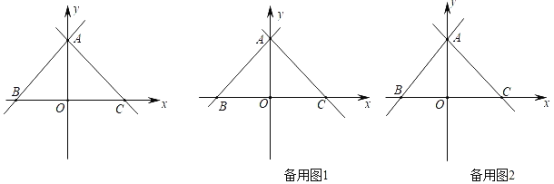
【题目】如图,在平面直角坐标系,点O是原点,直线y=x+6分别交x轴,y轴于点B,A,经过点A的直线y=﹣x+b交x轴于点 C.
(1)求b的值;
(2)点D是线段AB上的一个动点,连接OD,过点O作OE⊥OD交AC于点E,连接DE,将△ODE沿DE折叠得到△FDE,连接AF.设点D的横坐标为t,AF的长为d,当t>﹣3时,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,DE交OA于点G,且tan∠AGD=3.点H在x轴上(点H在点O的右侧),连接DH,EH,FH,当∠DHF=∠EHF时,请直接写出点H的坐标,不需要写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
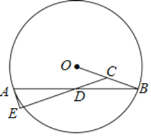
【题目】如图,在⊙O中,C,D分别为半径OB,弦AB的中点,连接CD并延长,交过点A的切线于点E.
(1)求证:AE⊥CE.
(2)若AE=2,sin∠ADE=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两条长度相等,且它们所在的直线互相垂直的线段,我们称其互为“等垂线段”.
知识应用:在△ABC和△ADE中,AC=BC,AE=DE,且AE<AC, ∠ACB=∠AED=90°,连接BD,点P是线段BD的中点,连接PC,PE.
(1)如图1,当AE在线段AC上时,线段PC与线段PE是否互为“等垂线段”?请说明理由.
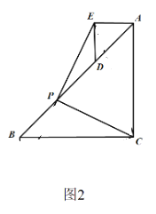
(2)如图2,将图1中的△ADE绕点A顺时针旋转90°,点D落在AB边上,请说明线段PC与线段PE互为“等垂线段”.
拓展延伸:(3)将图1中的△ADE绕点A顺时针旋转150°,若BC=3,DE=1,求PC的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com