
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长.(结果保留根号)

科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,
,![]() 交
交![]() 于另一点
于另一点![]() .
.
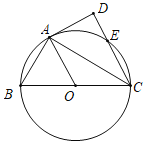
(1)求证:![]() ;
;
(2)若![]() 是
是![]() 上一动点,则
上一动点,则
①当![]()
![]() 时,以
时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形;
为顶点的四边形是正方形;
②当![]()
![]() 时,以
时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形.
为顶点的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的直径
的直径![]() ,
,![]() 、
、![]() 为圆周上两点,且
为圆周上两点,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
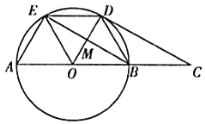
(1)求证:![]() 为
为![]() 切线;
切线;
(2)填空:①当四边形![]() 为菱形,则
为菱形,则![]() 的度数为________;
的度数为________;
②当![]() 时,四边形
时,四边形![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区购买甲、乙两种树苗进行绿化,购买一棵甲种树苗的价钱比购买一棵乙种树苗的价钱多 10 元钱,已知购买 20 棵甲种树苗、30 棵乙种树苗共需 1 200 元钱.
(1)求购买一棵甲种、一棵乙种树苗各多少元?
(2)社区决定购买甲、乙两种树苗共 400 棵,总费用不超过 10 600 元,那么该社区最多可以购买多少棵甲种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() . 点
. 点![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点, 连接
重合的任意一点, 连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]()
(1)动手操作
如图1,当![]() 时,我们通过用 刻度尺和量角器度量发现:
时,我们通过用 刻度尺和量角器度量发现:
![]() 的值是
的值是![]() ;直线
;直线![]() 与直线
与直线![]() 相交所成的较小角的度数是
相交所成的较小角的度数是![]() ;
;
请证明以上结论正确.
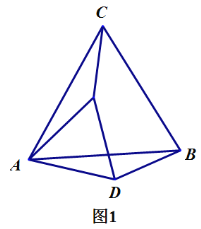
(2)类比探究
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并就图2的情形说明理由.
相交所成的较小角的度数,并就图2的情形说明理由.
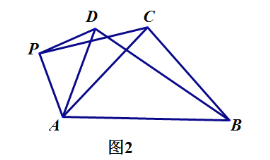
查看答案和解析>>
科目:初中数学 来源: 题型:
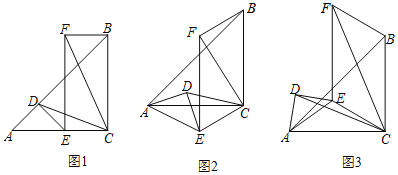
【题目】已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,以CE、BC为边作平行四边形CEFB,连CD、CF.
(1)如图1,当E、D分别在AC和AB上时,求证:CD=![]() CF;
CF;
(2)如图2,△ADE绕点A旋转一定角度,判断(1)中CD与CF的数量关系是否依然成立,并加以证明;
(3)如图3,AE=![]() ,AB=
,AB=![]() ,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,直接写出CF的长.
,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,直接写出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践 在![]() 中,
中,![]() ,点
,点![]() 为斜边
为斜边![]() 上的动点(不与点
上的动点(不与点![]() 重合).
重合).
(1)操作发现: 如图①,当![]() 时,把线段
时,把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
①![]() 的度数为________;
的度数为________;
②当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;

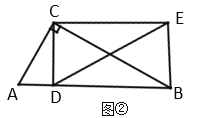
(2)探究证明: 如图②,当![]() 时,把线段
时,把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后并延长为原来的两倍, 记为线段
后并延长为原来的两倍, 记为线段![]() ,连接
,连接![]() .
.
①在点![]() 的运动过程中,请判断
的运动过程中,请判断![]() 与
与![]() 的大小关系,并证明;
的大小关系,并证明;
②当 时,求证:四边形
时,求证:四边形![]() 为矩形.
为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
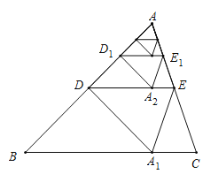
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() ,称为第
,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;还原纸片后,再将
;还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第
处,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;按上述方法不断操作下去…,经过第
;按上述方法不断操作下去…,经过第![]() 次操作后得到的折痕
次操作后得到的折痕![]() ,到
,到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com