
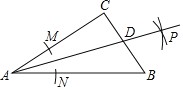
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,
,![]() 交
交![]() 于另一点
于另一点![]() .
.
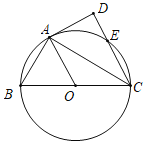
(1)求证:![]() ;
;
(2)若![]() 是
是![]() 上一动点,则
上一动点,则
①当![]()
![]() 时,以
时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形;
为顶点的四边形是正方形;
②当![]()
![]() 时,以
时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形.
为顶点的四边形是菱形.
【答案】(1)证明见解析;(2)①![]() ;②30°或
;②30°或![]() .
.
【解析】
(1)根据![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,
,![]() ,可得
,可得![]() =90°,
=90°,![]() =∠ACO,即可证明△ACD∽△BCA;
=∠ACO,即可证明△ACD∽△BCA;
(2)①若四边形A、O、C、D为正方形,可得∠AOC=90°,由OA=OC,得到∠OCA=∠OAC=45°,进而可得∠B=45°;
②若四边形A、O、C、E为菱形,分二种情况讨论:分点E与点A同侧;点E与点A异侧分别求解即可.
(1)证明:∵![]() 切
切![]() 于点
于点![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 是
是![]() 的直径,
的直径,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)①若四边形AOCD为正方形,
∴∠AOC=90°,
∵OA=OC,
∴∠OCA=∠OAC=45°,
∵∠BAC=90°,
∴∠B=90°-45°=45°,
故答案为:45°;
②若四边形A、O、C、E为菱形,分二种情况讨论:分点E与点A同侧;点E与点A异侧,
当点E与点A同侧时,连接AE,如图所示:
∵AD为切线,
∴∠DAE=∠ECA,∠OAD=90°,
∵AOCE为菱形,
∴∠OAC=∠EAC,
∴∠DAE=∠ECA=∠OAC=30°,
∴∠ACO=30°,∠AOB=∠ACO+∠OAC=30°+30°=60°,
∵OA=OB,
∴∠B=60°;
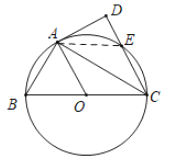
当点E与点A异侧时,如图所示:
∵AOEC是菱形,
∴AC=AO=OC,
∴△AOC是等边三角形,
∴∠AOC=60°,
∵AO=BO,
∴∠B=∠BAO=30°,
综上所述,∠B为30°或60°,
故答案为:30°或60°.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴是直线x=﹣1,且过点(1,0).顶点位于第二象限,其部分图象如图4所示,给出以下判断:①ab>0且c<0;②4a﹣2b+c>0;③8a+c>0;④c=3a﹣3b;⑤直线y=2x+2与抛物线y=ax2+bx+c两个交点的横坐标分别为x1,x2,则x1+x2+x1x2=5.其中正确的个数有( )
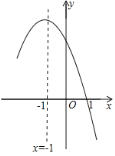
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 93 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙同学成绩的中位数;
(2)如果数与代数,空间与图形,统计与概率,综合与实践的成绩按4:3:1:2计算,那么甲、乙同学的数学综合素质成绩分别为多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
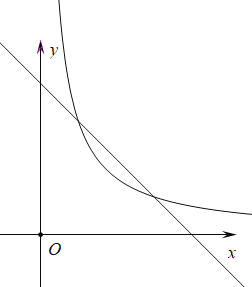
【题目】在平面直角坐标系xOy中,直线y=2x+b与双曲线![]() 交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线
交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线![]() 于点M,过点P作平行于y轴的直线交双曲线
于点M,过点P作平行于y轴的直线交双曲线![]() 于点N.
于点N.
(1)当点A的横坐标为1时,求b的值:
(2)在(1)的条件下,设P点的横坐标为m,
①若m=-1,判断PM与PN的数量关系,并说明理由;
②若PM<PN,结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°(AC>BC),用尺规作图的方法作线段AD,保留作图痕迹如图所示,认真观察作图痕迹,若CD=4,BD=5,则AC的长为( )
A.6B.9C.12D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+4x+c(a≠0)的图象与x轴交A,B两点,与y轴交于点C,直线y=﹣2x﹣6经过点A,C.
(1)求该二次函数的解析式;
(2)点P为第三象限内抛物线上的一个动点,△APC的面积为S,试求S的最大值;
(3)若P为抛物线的顶点,且直角三角形APQ的直角顶点Q在y轴上,请直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与函数
,与函数![]() 的图象的一个交点为
的图象的一个交点为![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)将线段![]() 向右平移得到对应线段
向右平移得到对应线段![]() ,当点
,当点![]() 落在函数
落在函数![]() 的图象上时,求线段
的图象上时,求线段![]() 扫过的面积.
扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com