
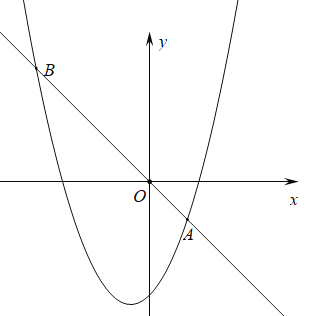
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与函数
,与函数![]() 的图象的一个交点为
的图象的一个交点为![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)将线段![]() 向右平移得到对应线段
向右平移得到对应线段![]() ,当点
,当点![]() 落在函数
落在函数![]() 的图象上时,求线段
的图象上时,求线段![]() 扫过的面积.
扫过的面积.
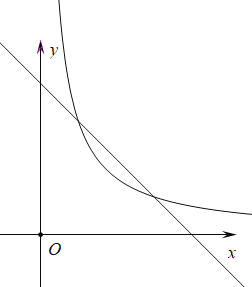
【答案】(1)m=4, n=1,k=3.(2)3.
【解析】
(1) 把点![]() ,分别代入直线
,分别代入直线![]() 中即可求出m=4,再把
中即可求出m=4,再把![]() 代入直线
代入直线![]() 即可求出n=1.把
即可求出n=1.把![]() 代入函数
代入函数![]() 求出k即可;
求出k即可;
(2)由(1)可求出点B的坐标为(0,4),点B‘是由点B向右平移得到,故点B’的纵坐标为4,把它代入反比例函数解析式即可求出它的横坐标,根据平移的知识可知四边形AA’B’B是平行四边形,再根据平行四边形的面积计算公式计算即可.
解:(1)把点![]() ,分别代入直线
,分别代入直线![]() 中得:
中得:
-4+m=0,![]()
m=4,
∴直线解析式为![]() .
.
把![]() 代入
代入![]() 得:
得:
n=-3+4=1.
∴点C的坐标为(3,1)
把(3,1)代入函数![]() 得:
得:
![]()
解得:k=3.
∴m=4, n=1,k=3.
(2)如图,设点B的坐标为(0,y)则y=-0+4=4
∴点B的坐标是(0,4)
当y=4时,![]()
解得,![]()
∴点B’(![]() ,4)
,4)
∵A’,B’是由A,B向右平移得到,
∴四边形AA’B’B是平行四边形,
故四边形AA’B’B的面积=![]()
![]() 4=3.
4=3.



科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的半径为 4,
的半径为 4,![]() 是圆的直径,点
是圆的直径,点![]() 是
是![]() 的切线
的切线![]() 上的一个动点,连接
上的一个动点,连接![]() 交
交![]() 于点
于点![]() ,弦
,弦![]() 平行于
平行于![]() ,连接
,连接![]() .
.
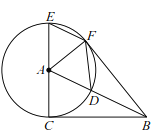
(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() __________时,四边形
__________时,四边形![]() 为菱形;
为菱形;
(3)当![]() ___________时,四边形
___________时,四边形![]() 为正方形.
为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
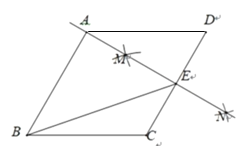
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于![]() 的同样的长为半径作弧,两弧交于M,N两点;
的同样的长为半径作弧,两弧交于M,N两点;
②作直线MN,交CD于点E,连接BE.
若直线MN恰好经过点A,则下列说法错误的是( )
A.ABC60°
B.![]()
C.若AB4,则BE![]()
D.tanCBE![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,
,![]() 交
交![]() 于另一点
于另一点![]() .
.
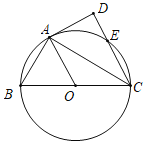
(1)求证:![]() ;
;
(2)若![]() 是
是![]() 上一动点,则
上一动点,则
①当![]()
![]() 时,以
时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形;
为顶点的四边形是正方形;
②当![]()
![]() 时,以
时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形.
为顶点的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,
,![]() .把抛物线
.把抛物线![]() 与线段
与线段![]() 围成的封闭图形记作
围成的封闭图形记作![]() .
.
(1)求此抛物线的解析式;
(2)点![]() 为图形
为图形![]() 中的抛物线上一点,且点
中的抛物线上一点,且点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴,交线段
轴,交线段![]() 于点
于点![]() .当
.当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]() 的值;
的值;
(3)点![]() 是直线
是直线![]() 上一点,且点
上一点,且点![]() 的横坐标为
的横坐标为![]() ,以线段
,以线段![]() 为边作正方形
为边作正方形![]() ,且使正方形
,且使正方形![]() 与图形
与图形![]() 在直线
在直线![]() 的同侧,当
的同侧,当![]() ,
,![]() 两点中只有一个点在图形
两点中只有一个点在图形![]() 的内部时,请直接写出
的内部时,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第![]() 天生产的防护服数量为
天生产的防护服数量为![]() 件,
件,![]() 与
与![]() 之间的关系可以用图中的函数图象来刻画.
之间的关系可以用图中的函数图象来刻画.

(1)直接写出![]() 与
与![]() 的函数关系式________;
的函数关系式________;
(2)由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第![]() 天创造的利润为
天创造的利润为![]() 元,直接利用(1)的结论,求
元,直接利用(1)的结论,求![]() 与
与![]() 之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实践小组想利用镜子的反射测量池塘边一棵树的高度AB.测量和计算的部分步骤如下:

①如图,树与地面垂直,在地面上的点C处放置一块镜子,小明站在BC的延长线上,当小明在镜子中刚好看到树的顶点A时,测得小明到镜子的距离CD=2米,小明的眼睛E到地面的距离ED=1.5米;
②将镜子从点C沿BC的延长线向后移动10米到点F处,小明向后移动到点H处时,小明的眼睛G又刚好在镜子中看到树的顶点A,这时测得小明到镜子的距离FH=3米;
③计算树的高度AB;
查看答案和解析>>
科目:初中数学 来源: 题型:
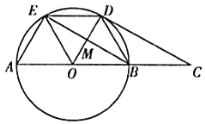
【题目】如图所示,![]() 的直径
的直径![]() ,
,![]() 、
、![]() 为圆周上两点,且
为圆周上两点,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 为
为![]() 切线;
切线;
(2)填空:①当四边形![]() 为菱形,则
为菱形,则![]() 的度数为________;
的度数为________;
②当![]() 时,四边形
时,四边形![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践 在![]() 中,
中,![]() ,点
,点![]() 为斜边
为斜边![]() 上的动点(不与点
上的动点(不与点![]() 重合).
重合).
(1)操作发现: 如图①,当![]() 时,把线段
时,把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
①![]() 的度数为________;
的度数为________;
②当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;

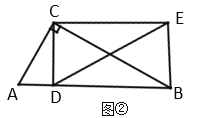
(2)探究证明: 如图②,当![]() 时,把线段
时,把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后并延长为原来的两倍, 记为线段
后并延长为原来的两倍, 记为线段![]() ,连接
,连接![]() .
.
①在点![]() 的运动过程中,请判断
的运动过程中,请判断![]() 与
与![]() 的大小关系,并证明;
的大小关系,并证明;
②当 时,求证:四边形
时,求证:四边形![]() 为矩形.
为矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com