
【题目】综合与实践 在![]() 中,
中,![]() ,点
,点![]() 为斜边
为斜边![]() 上的动点(不与点
上的动点(不与点![]() 重合).
重合).
(1)操作发现: 如图①,当![]() 时,把线段
时,把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
①![]() 的度数为________;
的度数为________;
②当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;

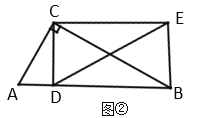
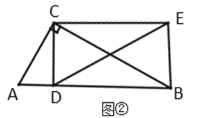
(2)探究证明: 如图②,当![]() 时,把线段
时,把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后并延长为原来的两倍, 记为线段
后并延长为原来的两倍, 记为线段![]() ,连接
,连接![]() .
.
①在点![]() 的运动过程中,请判断
的运动过程中,请判断![]() 与
与![]() 的大小关系,并证明;
的大小关系,并证明;
②当 时,求证:四边形
时,求证:四边形![]() 为矩形.
为矩形.
【答案】(1)①![]() ,②
,②![]() ;(2)①
;(2)①![]() ;证明见解析;②见解析.
;证明见解析;②见解析.
【解析】
(1)①由等腰三角形的性质得出∠A=∠ABC=45°,由旋转的性质得:∠ACD=∠BCE,CD=CE,证明△BCE≌△ACD,即可得出结果;
②由四边形![]() 为正方形,得BE=CD,∠CDB=90°,因为AC=BC,所以△ABC是等腰三角形,所以∠A=∠ABC=45°,解直角三角形可得CD的长,从而得到BE的长;
为正方形,得BE=CD,∠CDB=90°,因为AC=BC,所以△ABC是等腰三角形,所以∠A=∠ABC=45°,解直角三角形可得CD的长,从而得到BE的长;
(2)①证明△ACD∽△BCE,即可得出![]() ;
;
②由垂直的定义得出![]() ,由
,由![]() 得∠DBE=90°,因为
得∠DBE=90°,因为![]() ,所以得到四边形CDBE为矩形.
,所以得到四边形CDBE为矩形.
解:(1)①∵∠ACB=90°,AC=BC
∴∠A=∠ABC=45°
由旋转的性质得:∠ACD=∠BCE,CD=CE
在△BCE和△ACD中,
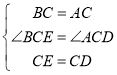
∴△BCE≌△ACD(SAS)
∴∠CBE=45°
②当BE=![]() 时,四边形
时,四边形![]() 为正方形.理由如下:
为正方形.理由如下:
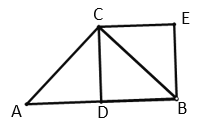
∵四边形![]() 为正方形
为正方形
∴BE=CD,∠CDB=90°
∴CD⊥AB
∵AC=BC=8
∴△ABC是等腰三角形
∴∠A=∠ABC=45°
∴CD=AC![]() sin45°=8×
sin45°=8×![]() =4
=4![]()
∴BE=4![]()
即当BE=![]() 时,四边形
时,四边形![]() 为正方形.
为正方形.
(2)①![]()
证明:如图,
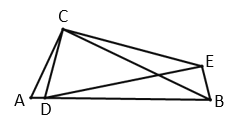
![]()
![]()
又![]()
![]()
![]()
![]()
![]()
②证明:由(2)①得![]()
![]()
![]()
![]()
又![]()
![]() 四边形
四边形![]() 是矩形
是矩形



 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
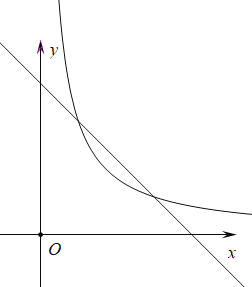
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与函数
,与函数![]() 的图象的一个交点为
的图象的一个交点为![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)将线段![]() 向右平移得到对应线段
向右平移得到对应线段![]() ,当点
,当点![]() 落在函数
落在函数![]() 的图象上时,求线段
的图象上时,求线段![]() 扫过的面积.
扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 将
将![]() 沿
沿![]() 所在的直线翻折,得到
所在的直线翻折,得到![]() 连接
连接![]() .
.
(1)若![]() 求抛物线的解析式.
求抛物线的解析式.
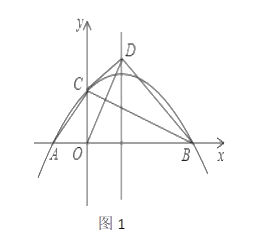
(2)如图1,设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,![]() 若
若![]() 点是半径为
点是半径为![]() 的
的![]() 上一动点,连接
上一动点,连接![]() 当点
当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的值最大,请求出这个最大值,并说明理由.
的值最大,请求出这个最大值,并说明理由.
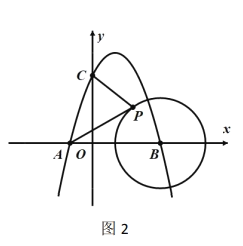
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,
,![]() 都是
都是![]() 的半径,过
的半径,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
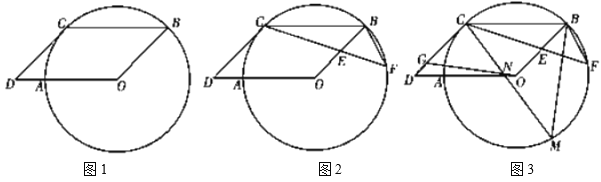
(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 在
在![]() 上,连接
上,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求证:四边形
,求证:四边形![]() 是平行四边形;
是平行四边形;
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() ,且
,且![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
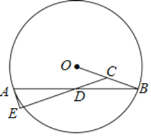
【题目】如图,在⊙O中,C,D分别为半径OB,弦AB的中点,连接CD并延长,交过点A的切线于点E.
(1)求证:AE⊥CE.
(2)若AE=2,sin∠ADE=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
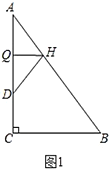
(1)如图1,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() ,若
,若![]() ,则
,则![]() ________.
________.
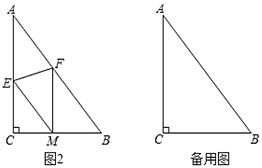
(2)如图2,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() .若
.若![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(3)在(1)(2)的条件下,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.
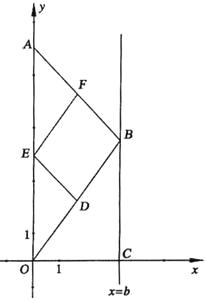
(1)判断四边形DEFB的形状.并证明你的结论;
(2)试求四边形DEFB的面积S与b的关系式;
(3)设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com