
【题目】如图所示,![]() 的直径
的直径![]() ,
,![]() 、
、![]() 为圆周上两点,且
为圆周上两点,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
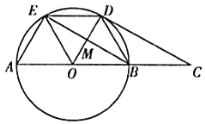
(1)求证:![]() 为
为![]() 切线;
切线;
(2)填空:①当四边形![]() 为菱形,则
为菱形,则![]() 的度数为________;
的度数为________;
②当![]() 时,四边形
时,四边形![]() 的面积为________.
的面积为________.
【答案】(1)见详解;(2)①30°;②![]()
【解析】
(1)根据题意可知,OD为半径,只需证明OD⊥DC即可;
(2)①若四边形AODE为菱形,可得出△AEO为等边三角形,结合∠AEB=90°,BE∥CD,得出∠C=∠ABE即可;
②根据条件![]() ,可证明△DOB为等边三角形,利用Rt△DOC和Rt△DON计算出△ODC的面积,以及菱形AODE的面积,相加即可得出四边形ACDE的面积.
,可证明△DOB为等边三角形,利用Rt△DOC和Rt△DON计算出△ODC的面积,以及菱形AODE的面积,相加即可得出四边形ACDE的面积.
(1)∵![]() ,
,
∴OD⊥BE,
∵BE∥CD,
∴OD⊥DC,
∵OD为半径,
∴CD为![]() 的切线;
的切线;
(2)①∵四边形AODE为菱形,
∴AE=OE=AO,
∴△AEO为等边三角形,
∴∠EAO=60°,
∵∠AEB=90°,
∴∠ABE=30°,
∵BE∥CD,
∴∠C=∠ABE=30°,
故答案为:30°;
②作DN⊥AC交AC于N,
∵DB=DO=OB=![]() AB,
AB,
∴△DOB为等边三角形,
∴∠DOB=60°,
在Rt△DOC和Rt△DON中,OD=2,∠DOC=60°,
∵DC=2![]() ,DN=
,DN=![]() ,∠C=30°,
,∠C=30°,
∴![]() ,
,
∵AODE为菱形,
∴![]() ,
,
∴四边形ACDE的面积=![]() +
+![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】甲乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 93 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙同学成绩的中位数;
(2)如果数与代数,空间与图形,统计与概率,综合与实践的成绩按4:3:1:2计算,那么甲、乙同学的数学综合素质成绩分别为多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
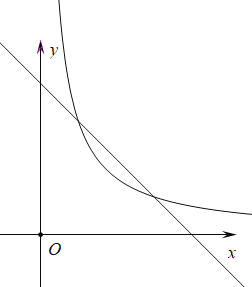
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与函数
,与函数![]() 的图象的一个交点为
的图象的一个交点为![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)将线段![]() 向右平移得到对应线段
向右平移得到对应线段![]() ,当点
,当点![]() 落在函数
落在函数![]() 的图象上时,求线段
的图象上时,求线段![]() 扫过的面积.
扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,点C,D在⊙O上,![]() 连接AD,OC.
连接AD,OC.
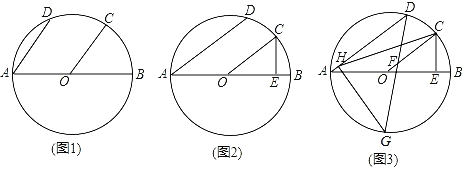
(1)如图1,求证:AD∥OC;
(2)如图2,过点C作CE⊥AB于点E,求证:AD=2OE;
(3)如图3,在(2)的条件下,点F在OC上,且OF=BE,连接DF并延长交⊙O于点G,过点G作CH⊥AD于点H,连接CH,若∠CFG=135°,CE=3,求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 将
将![]() 沿
沿![]() 所在的直线翻折,得到
所在的直线翻折,得到![]() 连接
连接![]() .
.
(1)若![]() 求抛物线的解析式.
求抛物线的解析式.
(2)如图1,设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
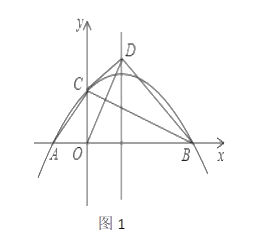
(3)如图2,![]() 若
若![]() 点是半径为
点是半径为![]() 的
的![]() 上一动点,连接
上一动点,连接![]() 当点
当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的值最大,请求出这个最大值,并说明理由.
的值最大,请求出这个最大值,并说明理由.
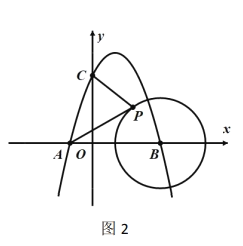
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
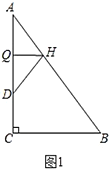
(1)如图1,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() ,若
,若![]() ,则
,则![]() ________.
________.
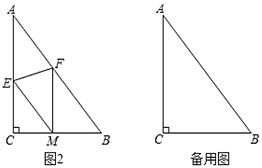
(2)如图2,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() .若
.若![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(3)在(1)(2)的条件下,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com