
【题目】甲乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 93 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙同学成绩的中位数;
(2)如果数与代数,空间与图形,统计与概率,综合与实践的成绩按4:3:1:2计算,那么甲、乙同学的数学综合素质成绩分别为多少分?
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系网格中,三角形![]() 的顶点坐标分别是
的顶点坐标分别是![]() .将三角形
.将三角形![]() 平移,使顶点
平移,使顶点![]() 平移到坐标原点
平移到坐标原点![]() 处,得到三角形
处,得到三角形![]() .
.
(1)![]() 的坐标是________,
的坐标是________,![]() 的坐标是________.
的坐标是________.
(2)画出平移后的![]() .
.
(3)求![]() 的面积。
的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
(1) 表中a=__________,b=__________,c=__________
(2) 请补全频数分布直方图;
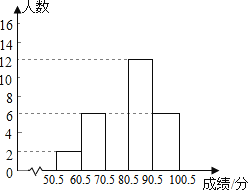
组别 | 分数段/分 | 频数/人数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |
(3) 该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
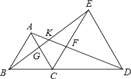
【题目】如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于点F,BE交AC于点G,则图中可通过旋转而相互得到的三角形有 对.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:如图,用同样大小的黑色棋子按如图所示的规律摆放,它们的棋子数依次表示为 a1,a2,a3,a4,…,an.
 …
…
请你认真观察上面四个图案,从中发现规律,并试着解答下列问题:
(1)写出 a1,a2,a3,a4 的值;
(2)求 a7 的值;
(3)用 n 表示出 an,并判断第几个图案有 6055 个黑色棋子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
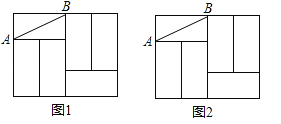
(1)在图1中画出一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;
(2)在图2中画出线段AB的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并解决问题:归纳
人们通过长期观察发现,如果早晨天空中有棉絮状的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学里,我们也常用这样的方法探求规律,例如:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点,把三角形剪成若干个小三角形,那么最多可以剪得多少个这样的三角形? .为了解决这个问题,我们可以从n=1、n=2、nr=3 等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.

(1)完成表格信息:_______、_________;
(2)通过观察、比较,可以发现:三角形内的点每增加1个,最多可以剪得的三角形增加_________个.于是,我们可以猜想:当三角形内的点的个数为n时,最多可以剪得____________个三角形.像这样通过对现象的观察、分析,从特殊到-般地探索这类现象的规律、提出猜想的思想方法称为归纳.在日常生活中,人们互相交谈时,常常有人在列举了一些现象后,说“这(即列举的现象)说明....其实这就是运用了归纳的方法.用归纳的方法得出的结论不一定正确,是否正确需要加以证实.
(3)请你借助表格尝试用归纳的方法探索: 1+3+5+7+......+(2n-1)的和是多少?并加以证实.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com