
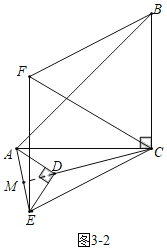
°æƒø°ø“—÷™°˜ACB∫Õ°˜ADE∂º «µ»—¸÷±Ω«»˝Ω«–Œ£¨°œACB£Ω°œADE£Ω90°„£¨“‘CE°¢BCŒ™±fl◊˜∆Ω––Àƒ±fl–ŒCEFB£¨¡¨CD°¢CF£Æ
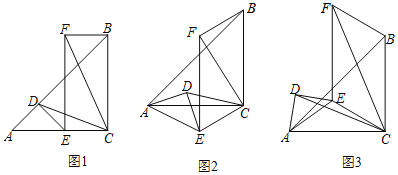
£®1£©»ÁÕº1£¨µ±E°¢D∑÷±‘⁄AC∫ÕAB…œ ±£¨«Û÷§£∫CD£Ω![]() CF£ª
CF£ª
£®2£©»ÁÕº2£¨°˜ADE»∆µ„A–˝◊™“ª∂®Ω«∂»£¨≈–∂œ£®1£©÷–CD”ÎCFµƒ ˝¡øπÿœµ «∑Ò“¿»ª≥…¡¢£¨≤¢º”“‘÷§√˜£ª
£®3£©»ÁÕº3£¨AE£Ω![]() £¨AB£Ω
£¨AB£Ω![]() £¨Ω´°˜ADE»∆Aµ„–˝◊™“ª÷‹£¨µ±Àƒ±fl–ŒCEFBŒ™¡‚–Œ ±£¨÷±Ω”–¥≥ˆCFµƒ≥§£Æ
£¨Ω´°˜ADE»∆Aµ„–˝◊™“ª÷‹£¨µ±Àƒ±fl–ŒCEFBŒ™¡‚–Œ ±£¨÷±Ω”–¥≥ˆCFµƒ≥§£Æ
°æ¥∞∏°ø£®1£©œÍº˚Ω‚Œˆ£ª£®2£©≥…¡¢£¨¿Ì”…œÍº˚Ω‚Œˆ£ª£®3£©CFµƒ÷µŒ™6ªÚ4£Æ
°æΩ‚Œˆ°ø
£®1£©¡¨Ω”FD£Æ÷§√˜°˜ADC°’°˜EDF£®SAS£©£¨Õ∆≥ˆ°˜DFCŒ™µ»—¸÷±Ω«»˝Ω«–Œº¥ø…Ω‚æˆŒ £ª
£®2£©≥…¡¢£¨¡¨Ω”FD£¨÷§√˜°˜ADC°’°˜EDF£®SAS£©£¨Õ∆≥ˆ°˜DFCŒ™µ»—¸÷±Ω«»˝Ω«–Œº¥ø…Ω‚æˆŒ £ª
£®3£©∑÷¡Ω÷÷«È–Œ∑÷±ª≠≥ˆÕº–Œ£¨¿˚”√£®2£©÷–Ω·¬€«Û≥ˆCDº¥ø…Ω‚æˆŒ £Æ
£®1£©÷§√˜£∫¡¨Ω”FD£¨
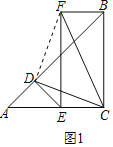
°flAD£ΩED£¨°œADE£Ω90°„£¨
°‡°œDAC£Ω°œAED£Ω45°„£¨
°flÀƒ±fl–ŒBCEF «∆Ω––Àƒ±fl–Œ£¨°œBCE£Ω90°„£¨
°‡Àƒ±fl–ŒBCEF «æÿ–Œ£¨
°‡°œCEF£Ω°œAEF£Ω90°„£¨BC£ΩEF£ΩAC£¨
°‡°œDEF£Ω45°„£¨
°‡°œA£Ω°œDEF£¨
°‡°˜ADC°’°˜EDF£®SAS£©£¨
°‡DC£ΩDF£¨°œDCA£Ω°œDFE£¨
°‡°œFDC£Ω°œFEC£Ω90°„£¨¥”∂¯°˜DFCŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨
°‡CD£Ω![]() CF£ª
CF£ª
£®2£©Ω‚£∫≥…¡¢£Æ
¿Ì”…£∫¡¨Ω”FD£¨
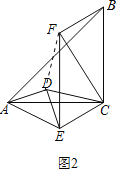
°flAD°ÕDE£¨EF°ÕAC£¨
°‡°œDAC£Ω°œDEF£¨”÷AD£ΩED£¨AC£ΩEF£¨
°‡°˜ADC°’°˜EDF£®SAS£©£¨
°‡DC£ΩDF£¨°œADC£Ω°œEDF£¨º¥°œADE+°œEDC£Ω°œFDC+°œEDC£¨
°‡°œFDC£Ω°œADE£Ω90°„£¨
°‡°˜DFCŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨
°‡CD£Ω![]() CF£ª
CF£ª
£®3£©Ω‚£∫»ÁÕº3©Å1÷–£¨…ËAE”ÎCDµƒΩªµ„Œ™M£¨
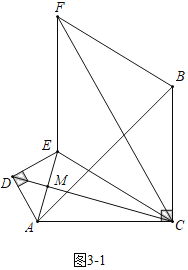
°flCE£ΩCA£¨DE£ΩDA£¨
°‡CD¥π÷±∆Ω∑÷AE£¨
°‡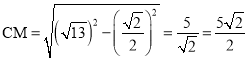 £¨DM£Ω
£¨DM£Ω![]() £¨
£¨
°‡CD£ΩDM+CM£Ω![]() £¨
£¨
°flCF£Ω![]() CD
CD
°‡CF£Ω6£ª
»ÁÕº3©Å2÷–£¨…ËAE”ÎCDµƒΩªµ„Œ™M£¨
Õ¨∑®ø…µ√CD£ΩCM©ÅDM£Ω![]() £¨
£¨
°‡CF£Ω![]() CD£Ω4£¨
CD£Ω4£¨
◊€…œÀ˘ ˆ£¨¬˙◊„Ãıº˛µƒCFµƒ÷µŒ™6ªÚ4£Æ



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝y£Ωax2+4x+c£®a°Ÿ0£©µƒÕºœÛ”Îx÷·ΩªA£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨÷±œfly£Ω©Å2x©Å6æ≠π˝µ„A£¨C£Æ
£®1£©«Û∏√∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©µ„PŒ™µ⁄»˝œÛœfiƒ⁄≈◊ŒÔœfl…œµƒ“ª∏ˆ∂ص„£¨°˜APCµƒ√ʪ˝Œ™S£¨ ‘«ÛSµƒ◊Ó¥Û÷µ£ª
£®3£©»ÙPŒ™≈◊ŒÔœflµƒ∂•µ„£¨«“÷±Ω«»˝Ω«–ŒAPQµƒ÷±Ω«∂•µ„Q‘⁄y÷·…œ£¨«Î÷±Ω”–¥≥ˆµ„Qµƒ◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„![]() °¢µ„
°¢µ„![]() ‘⁄∞Îæ∂Œ™
‘⁄∞Îæ∂Œ™![]() µƒ
µƒ![]() …œ£¨
…œ£¨![]() Œ™
Œ™![]() …œ“ª∂ص„£¨
…œ“ª∂ص„£¨![]() Œ™
Œ™![]() ÷·…œ“ª∂®µ„£¨
÷·…œ“ª∂®µ„£¨![]() «“
«“![]() µ±µ„
µ±µ„![]() ¥”
¥”![]() µ„ƒÊ ±’ΑÀ∂صΩ
µ„ƒÊ ±’ΑÀ∂صΩ![]() µ„ ±£¨
µ„ ±£¨![]() µ„µƒ‘À∂ج∑æ∂≥§ «(°°°°)
µ„µƒ‘À∂ج∑æ∂≥§ «(°°°°)
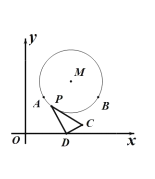
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™º”øÏ≥«œÁ∂‘Ω”£¨Ω®…Ë»´”Ú√¿¿ˆœÁ¥Â£¨ƒ≥µÿ«¯∂‘![]() ¡Ωµÿº‰µƒπ´¬∑Ω¯––∏ƒΩ®£Æ»ÁÕº£¨
¡Ωµÿº‰µƒπ´¬∑Ω¯––∏ƒΩ®£Æ»ÁÕº£¨![]() ¡Ωµÿ÷ƺ‰”–“ª◊˘…Ω£¨∆˚≥µ‘≠¿¥¥”
¡Ωµÿ÷ƺ‰”–“ª◊˘…Ω£¨∆˚≥µ‘≠¿¥¥”![]() µÿµΩ
µÿµΩ![]() µÿ–ËÕææ∂
µÿ–ËÕææ∂![]() µÿ—ÿ’€œfl
µÿ—ÿ’€œfl![]() –– ª£¨œ÷ø™Õ®À̵¿∫Û£¨∆˚≥µø…÷±Ω”—ÿ÷±œfl
–– ª£¨œ÷ø™Õ®À̵¿∫Û£¨∆˚≥µø…÷±Ω”—ÿ÷±œfl![]() –– ª£Æº∫÷™
–– ª£Æº∫÷™![]() «ß√◊£¨
«ß√◊£¨![]() £Æ £®Ω·π˚æ´»∑µΩ
£Æ £®Ω·π˚æ´»∑µΩ![]() «ß√◊£¨≤Œøº ˝æ›£∫
«ß√◊£¨≤Œøº ˝æ›£∫![]() £©
£©

£®1£©ø™Õ®À̵¿«∞£¨∆˚≥µ¥”![]() µÿµΩ
µÿµΩ![]() µÿ¥Û‘º“™◊fl∂‡…Ÿ«ß√◊?
µÿ¥Û‘º“™◊fl∂‡…Ÿ«ß√◊?
£®2£©ø™Õ®À̵¿∫Û£¨∆˚≥µ¥”![]() µÿµΩ
µÿµΩ![]() µÿ¥Û‘ºø…“‘…Ÿ◊fl∂‡…Ÿ«ß√◊?
µÿ¥Û‘ºø…“‘…Ÿ◊fl∂‡…Ÿ«ß√◊?
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÀÊ◊≈ÃÏ∆¯µƒ÷Ω•—◊»»£®»ÁÕº1£©£¨’⁄—Ù…°‘⁄Œ“√«µƒ»’≥£…˙ªÓ÷–ÀÊ¥¶ø…º˚»ÁÕº2À˘ 棨’⁄—Ù…°¡¢÷˘OA¥π÷±”⁄µÿ√Ê£¨µ±Ω´’⁄—Ù…°≥≈ø™÷¡ODŒª÷√ ±£¨≤‚µ√°œODB£Ω45°„£¨µ±Ω´’⁄—Ù…°≥≈ø™÷¡OEŒª÷√ ±£¨≤‚µ√°œOEC£Ω30°„£¨«“¥À ±’⁄—Ù…°±fl—ÿ…œ…˝µƒ ˙÷±∏fl∂»BCŒ™20cm£¨«Û»Ùµ±’⁄—Ù…°≥≈ø™÷¡OEŒª÷√ ±…°œ¬“ı¡π√ʪ˝◊Ó¥Û£¨«Û¥À ±…°œ¬∞Îæ∂ECµƒ≥§£Æ£®Ω·π˚±£¡Ù∏˘∫≈£©

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°∂∞Ò—˘‘ƒ∂¡°∑ «÷–π˙«‡ƒÍ±®°§÷–«‡‘⁄œfl¡™∫œø·Œ““Ù¿÷π≤Õ¨¥Ú‘ϵƒ ◊µµ«‡ƒÍ‘ƒ ∂¡∑÷œÌ¿‡“Ù∆µΩ⁄ƒø£¨«‡¥∫≈ºœÒ¥´ÀÃæ≠µ‰°¢Ω≤ ˆ≥…≥§π ¬£¨”√…˘“Ùœ∆∆–¬ ±¥˙«‡ƒÍ‘ƒ∂¡»»≥±£Æƒ≥ ÷–—ߌ™¡À¬˙◊„—ß…˙µƒ‘ƒ∂¡–Ë«Û£¨π∫Ω¯¡À“ª≈˙Õº È£¨≤¢«∞∫Û¡Ω¥Œπ∫¬Ú¡Ω÷÷ Ⱥ‹£¨∆‰÷–µ⁄“ª¥Œπ∫ ¬ÚÃ˙÷ Ⱥ‹![]() ∏ˆ£¨ƒæ÷ Ⱥ‹
∏ˆ£¨ƒæ÷ Ⱥ‹![]() ∏ˆ£¨π≤ª®∑—
∏ˆ£¨π≤ª®∑—![]() ‘™£ªµ⁄∂˛¥Œπ∫¬ÚÃ˙÷ Ⱥ‹
‘™£ªµ⁄∂˛¥Œπ∫¬ÚÃ˙÷ Ⱥ‹![]() ∏ˆ£¨ƒæ÷ Ⱥ‹
∏ˆ£¨ƒæ÷ Ⱥ‹![]() ∏ˆ£¨π≤ª®∑—
∏ˆ£¨π≤ª®∑—![]() ‘™£¨«“¡Ω¥Œπ∫¬Úµƒ¡Ω÷÷ Ⱥ‹µ•º€≤ª±‰£Æ
‘™£¨«“¡Ω¥Œπ∫¬Úµƒ¡Ω÷÷ Ⱥ‹µ•º€≤ª±‰£Æ
£®1£©«Û’‚¡Ω÷÷ Ⱥ‹µƒµ•º€∑÷±Œ™∂‡…Ÿ‘™£ø
£®2£©»Ù∏√—ß–£º∆ªÆ‘Ÿ¥Œπ∫¬Ú’‚¡Ω÷÷ Ⱥ‹π≤![]() ∏ˆ£¨«““™«ÛÃ˙÷ Ⱥ‹µƒ ˝¡ø≤ª∂‡”⁄ƒæ÷ Ⱥ‹ ˝ ¡øµƒ
∏ˆ£¨«““™«ÛÃ˙÷ Ⱥ‹µƒ ˝¡ø≤ª∂‡”⁄ƒæ÷ Ⱥ‹ ˝ ¡øµƒ![]() ±∂£¨«Î…˺∆≥ˆ◊Ó °«Æµƒπ∫¬Ú∑Ω∞∏£¨≤¢«Û≥ˆ◊Ó…Ÿ∑—”√£Æ
±∂£¨«Î…˺∆≥ˆ◊Ó °«Æµƒπ∫¬Ú∑Ω∞∏£¨≤¢«Û≥ˆ◊Ó…Ÿ∑—”√£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() ∂º «
∂º «![]() µƒ∞Îæ∂£¨π˝
µƒ∞Îæ∂£¨π˝![]() ◊˜
◊˜![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() µƒ«–œflΩª
µƒ«–œflΩª![]() µƒ—”≥§œfl”⁄µ„
µƒ—”≥§œfl”⁄µ„![]() £Æ
£Æ
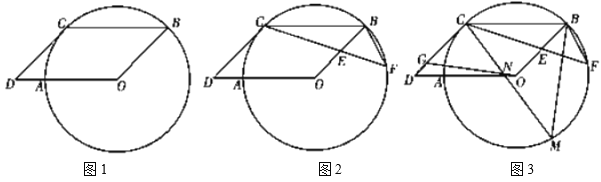
£®1£©»ÁÕº1£¨«Û÷§£∫![]() £ª
£ª
£®2£©»ÁÕº2£¨µ„![]() ‘⁄
‘⁄![]() …œ£¨¡¨Ω”
…œ£¨¡¨Ω”![]() ≤¢—”≥§Ωª
≤¢—”≥§Ωª![]() ”⁄µ„
”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨»Ù
£¨»Ù![]() £¨«Û÷§£∫Àƒ±fl–Œ
£¨«Û÷§£∫Àƒ±fl–Œ![]() «∆Ω––Àƒ±fl–Œ£ª
«∆Ω––Àƒ±fl–Œ£ª
£®3£©»ÁÕº3£¨‘⁄£®2£©µƒÃıº˛œ¬£¨µ„![]() ‘⁄
‘⁄![]() …œ£¨¡¨Ω”
…œ£¨¡¨Ω”![]() £¨«“
£¨«“![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() …œ£¨¡¨Ω”
…œ£¨¡¨Ω”![]() £¨
£¨![]() £¨
£¨![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨«“
£¨«“![]() £¨»Ù
£¨»Ù![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ≥§£Æ
µƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨÷±œfl![]() ∑÷±”Î
∑÷±”Î![]() ÷·°¢
÷·°¢![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() ¡Ωµ„£¨µ„
¡Ωµ„£¨µ„![]() ‘⁄
‘⁄![]() ÷·…œ£¨
÷·…œ£¨![]() £¨≈◊ŒÔœfl
£¨≈◊ŒÔœfl![]() æ≠π˝
æ≠π˝![]() ¡Ωµ„£Æ
¡Ωµ„£Æ
£®1£©«Û![]() ¡Ωµ„µƒ◊¯±Í£ª
¡Ωµ„µƒ◊¯±Í£ª
£®2£©«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
£®3£©µ„![]() «÷±œfl
«÷±œfl![]() …œ∑Ω≈◊ŒÔœfl…œµƒ“ªµ„£¨π˝µ„
…œ∑Ω≈◊ŒÔœfl…œµƒ“ªµ„£¨π˝µ„![]() ◊˜
◊˜![]() ”⁄µ„
”⁄µ„![]() £¨◊˜
£¨◊˜![]() ÷·Ωª
÷·Ωª![]() ”⁄µ„
”⁄µ„![]() £¨«Û
£¨«Û![]() ÷‹≥§µƒ◊Ó¥Û÷µ£Æ
÷‹≥§µƒ◊Ó¥Û÷µ£Æ
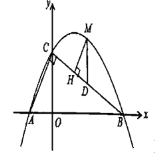
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨°œACB£Ω90°„£¨BC£Ω3£¨AC£Ω4£¨G «±flABµƒ÷–µ„£¨∆Ω––”⁄ABµƒ∂Ø÷±œfll∑÷±Ωª°˜ABCµƒ±flCA°¢CB”⁄µ„M°¢N£¨…ËCM£Ωm.
£®1£©µ±m£Ω1 ±£¨«Û°˜MNGµƒ√ʪ˝£ª
£®2£©»Ùµ„Gπÿ”⁄÷±œfllµƒ∂‘≥∆µ„Œ™µ„G°‰£¨«Î«Û≥ˆµ„G°‰ «°∫√¬‰‘⁄°˜ABCµƒƒ⁄≤ø£®≤ª∫¨±flΩÁ£© ±£¨mµƒ»°÷µ∑∂Œß£ª
£®3£©°˜MNG «∑Òø…ƒ‹Œ™÷±Ω«»˝Ω«–Œ£ø»Áπ˚ƒ‹£¨«Î«Û≥ˆÀ˘”–∑˚∫œÃıº˛µƒmµƒ÷µ£ª»Áπ˚≤ªƒ‹£¨«ÎÀµ√˜¿Ì”….

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com