
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点
轴交点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .如图1,点
.如图1,点![]() 为抛物线上任意一点,过点
为抛物线上任意一点,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() .
.
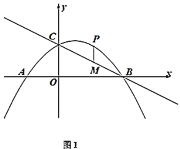
(1)求抛物线的解析式;
(2)当![]() 是直角三角形时,求
是直角三角形时,求![]() 点坐标;
点坐标;
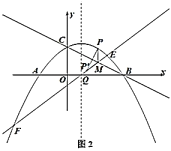
(3)如图2,作![]() 点关于直线
点关于直线![]() 的对称点
的对称点![]() ,作直线
,作直线![]() 与抛物线交于
与抛物线交于![]() ,设抛物线对称轴与
,设抛物线对称轴与![]() 轴交点为
轴交点为![]() ,当直线
,当直线![]() 经过点
经过点![]() 时,请你直接写出
时,请你直接写出![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3) 2
;(3) 2![]() .
.
【解析】
(1)先求出A、C点的坐标,然后用待定系数法确定抛物线的解析式即可;
(2)设![]() ,则
,则![]() ,然后就P在BC上方和下方分别解答即可;
,然后就P在BC上方和下方分别解答即可;
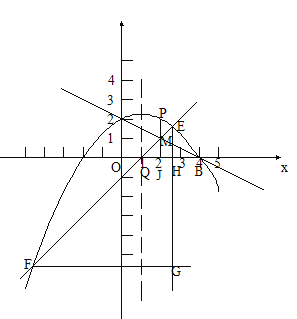
(3)由题意得B、C两点的坐标分别为(4,0)和(0,2),求得M和Q的坐标,得出直线QM的解析式,进而确定E、F两点的横坐标和纵坐标;然后过点E做垂直于x轴的直线交点为H,过点F做垂直于y轴的直线,交于点G ,证得△EQH∽△EFG和△MQJ∽△EQH,然后运用相似三角形的性质列出方程解答即可.
解:(1)在![]() 中,当
中,当![]() 时
时![]() ,当
,当![]() 时
时![]() ,∴
,∴![]() 、
、![]()
∵抛物线![]() 的图象经过
的图象经过![]() ,
,![]() 两点
两点
∴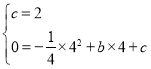
∴![]()
∴抛物线的解析式为![]()
(2)设![]() ,则
,则![]()
①当![]() 在
在![]() 的上方时,
的上方时,
![]() ,
,![]()
若![]() ,
,
∵![]() 轴,可得
轴,可得![]() 轴
轴
∴![]()
∴![]()
在![]() 中
中![]()
∴在![]() 中,
中,![]()
∴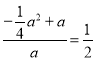
∴![]() 或
或![]() (舍去)
(舍去)
∴![]() 点坐标
点坐标![]()
②当![]() 在
在![]() 的下方时,过
的下方时,过![]() 作
作![]() 于
于![]() .
.
若![]() ,
,![]()
![]()
![]()
∴![]()
∴在![]() 中,
中,![]()
∴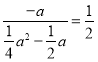 .
.
∴![]() 或
或![]() (舍去)
(舍去)
∴![]() 点坐标
点坐标![]()
∴当![]() 是直角三角形时,
是直角三角形时,![]() 点坐标为
点坐标为![]() 或
或![]() .
.
(3)设BC直线为y=kx+b,
有![]() 解得导
解得导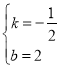 ,
,
∴直线BC为![]()
抛物线的解析式可化为:![]() ,
,
∴点Q坐标为(1,0)
∵PM⊥x轴
∴点M横坐标即为点P横坐标,为2
又∵点M在直线BC上,有![]() =1
=1
∴点M坐标为(2,1)
设过点Q、M直线为y=k2x+b2,
则有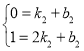 ,解得
,解得
∴ QM直线为y=x-1
由 解得
解得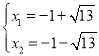
∴E、F横坐标别为Ex=![]() ,Fx=
,Fx=![]()
又∵点E、F在QM直线上,
∴点E、F别坐标为Ey=![]() ,Fy=
,Fy=![]()
过点E作垂直于x轴的直线交点为H,过点F作垂直于y 轴的直线,交于点G
∵EH⊥x轴,FG⊥y轴
∴EH⊥FG,G点坐标为(Ex,Fy)
∴∠EHQ=∠EGF=90°
又∵∠EQH=∠EFG
△EQH∽△EFG
过点M作垂直于x轴的直线交点为J
同理可得△MQJ∽△EQH,
∴△EQH∽△EFG△MQJ,
∴![]()
∴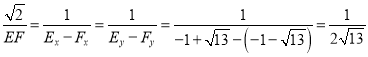
∴EF=![]() ×
×![]() =2
=2![]()


科目:初中数学 来源: 题型:
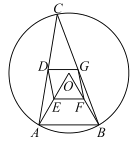
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
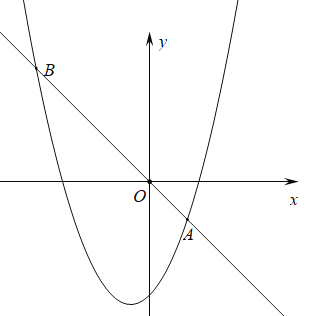
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点A,它的顶点为点B.
与y轴交于点A,它的顶点为点B.
(1)点A的坐标为______,点B的坐标为______(用m表示);
(2)已知点M(-6,4),点N(3,4),若抛物线与线段MN恰有一个公共点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,
,![]() .把抛物线
.把抛物线![]() 与线段
与线段![]() 围成的封闭图形记作
围成的封闭图形记作![]() .
.
(1)求此抛物线的解析式;
(2)点![]() 为图形
为图形![]() 中的抛物线上一点,且点
中的抛物线上一点,且点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴,交线段
轴,交线段![]() 于点
于点![]() .当
.当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]() 的值;
的值;
(3)点![]() 是直线
是直线![]() 上一点,且点
上一点,且点![]() 的横坐标为
的横坐标为![]() ,以线段
,以线段![]() 为边作正方形
为边作正方形![]() ,且使正方形
,且使正方形![]() 与图形
与图形![]() 在直线
在直线![]() 的同侧,当
的同侧,当![]() ,
,![]() 两点中只有一个点在图形
两点中只有一个点在图形![]() 的内部时,请直接写出
的内部时,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生体育测试中跳绳成绩的情况,随机抽取该校九年级若干名男生,调查他们的跳绳成绩![]() (次/分),按成绩分成
(次/分),按成绩分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级.将所得数据绘制成如下统计图.根据图中信息,解答下列问题:
五个等级.将所得数据绘制成如下统计图.根据图中信息,解答下列问题:
该校被抽取的男生跳绳成绩频数分布直方图
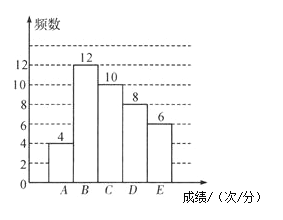
(1)本次调查中,男生的跳绳成绩的中位数在________等级;
(2)若该校九年级共有男生400人,估计该校九年级男生跳绳成绩是![]() 等级的人数.
等级的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实践小组想利用镜子的反射测量池塘边一棵树的高度AB.测量和计算的部分步骤如下:

①如图,树与地面垂直,在地面上的点C处放置一块镜子,小明站在BC的延长线上,当小明在镜子中刚好看到树的顶点A时,测得小明到镜子的距离CD=2米,小明的眼睛E到地面的距离ED=1.5米;
②将镜子从点C沿BC的延长线向后移动10米到点F处,小明向后移动到点H处时,小明的眼睛G又刚好在镜子中看到树的顶点A,这时测得小明到镜子的距离FH=3米;
③计算树的高度AB;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
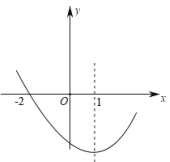
【题目】如图,二次函数![]() 的图象过点
的图象过点![]() ,对称轴为直
,对称轴为直![]() 线,下列结论中一定正确的是____________(填序号即可).
线,下列结论中一定正确的是____________(填序号即可).
①![]() ;
;
②若![]() 是抛物线上的两点,当
是抛物线上的两点,当![]() 时,
时,![]()
③若方程![]() 的两根为
的两根为![]() ,且
,且![]() ,则
,则![]()
④![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com