
【题目】如图,在不是菱形的平行四边形![]() 中,
中,![]() 在对角线
在对角线![]() 上,在以下三个条件中再选一个,①
上,在以下三个条件中再选一个,①![]() 分别是
分别是![]() 的中线,②
的中线,②![]() 分别是
分别是![]() 的角平分线,③
的角平分线,③![]() .使得四边形
.使得四边形![]() 是平行四边形,并说明理由.
是平行四边形,并说明理由.

【答案】选②能使得四边形![]() 是平行四边形,理由见详解.
是平行四边形,理由见详解.
【解析】
对三个条件进行逐一分析,利用平行四边形的判定方法验证是否能使四边形![]() 是平行四边形,如果能,则可以选择,如果不能,则不能选择.
是平行四边形,如果能,则可以选择,如果不能,则不能选择.
选②能使得四边形![]() 是平行四边形,理由如下:
是平行四边形,理由如下:
∵四边形ABCD是平行四边形,且不是菱形,
∴![]() ,对角线AC不平分对角
,对角线AC不平分对角![]() ,
,
![]() .
.
∵AE平分![]() ,CF平分
,CF平分![]() ,
,
∴![]() ,且AE,CF不在同一直线上.
,且AE,CF不在同一直线上.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
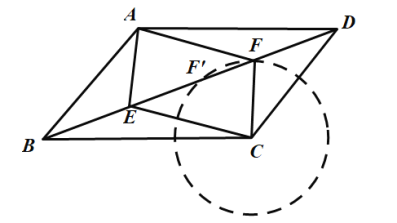
中,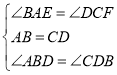
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
∴四边形AECF是平行四边形;
选择①不能使四边形AECF是平行四边形,理由如下:
∵四边形ABCD是平行四边形,
∴AC,BD互相平分,
∴若![]() 分别是
分别是![]() 的中线,则AE,CF在同一条直线上,不存在四边形AECF,故不能选①;
的中线,则AE,CF在同一条直线上,不存在四边形AECF,故不能选①;
选③不一定能使四边形AECF是平行四边形,理由是:
∵![]() ,AE与CF不一定平行,
,AE与CF不一定平行,
如图中AE与![]() 相等但不平行,
相等但不平行,
∴四边形AECF不一定是平行四边形,故不能选③.


科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项.现随机抽查了部分学生,并将其结果绘制成如下不完整的条形图和扇形图.
抽取的学生最喜欢体育活动的条形统计图
抽取的学生最喜欢体育活动的扇形统计图
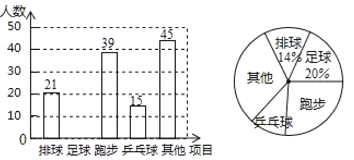
请结合以上信息解答下列问题:
(1)在这次调查中一共抽查了_____学生,扇形统计图中“乒乓球”所对应的圆心角为_____度,并请补全条形统计图;
(2)己知该校共有1200名学生,请你估计该校最喜爱跑步的学生人数;
(3)若在“排球、足球、跑步、乒乓球”四个活动项目任选两项设立课外兴趣小组,请用列表法或画树状图的方法求恰好选中“排球、乒乓球”这两项活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
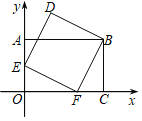
A. (1,2.5)B. (1,1+ ![]() )C. (1,3)D. (
)C. (1,3)D. (![]() ﹣1,1+
﹣1,1+ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
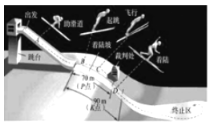
【题目】跳台滑雪是冬季奥运会比赛项目之一,如图平面直角坐标系是跳台滑雪的截面示意图,运动员沿滑道![]() 下滑,在
下滑,在![]() 轴上的点
轴上的点![]() 起跳,点
起跳,点![]() 距落地水平面
距落地水平面![]() 轴
轴![]() ,运动员落地的雪面开始是一段曲线
,运动员落地的雪面开始是一段曲线![]() ,到达点
,到达点![]() 后变为水平面,点
后变为水平面,点![]() 距
距![]() 轴的水平距离为
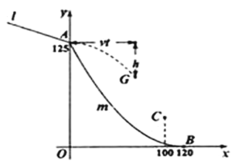
轴的水平距离为![]() .运动员(看成点)从点
.运动员(看成点)从点![]() 起跳后的水平速度为
起跳后的水平速度为![]() ,点
,点![]() 是下落路线的某位置.忽略空气阻力,实验表明:
是下落路线的某位置.忽略空气阻力,实验表明:![]() ,
,![]() 的竖直距离
的竖直距离![]() 与飞出时间
与飞出时间![]() 的平方成正比,且
的平方成正比,且![]() 时
时![]() ;
;![]() ,
,![]() 的水平距离是
的水平距离是![]() 米.
米.
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)用含![]() 、
、![]() 的代数式表示点
的代数式表示点![]() 的横坐标
的横坐标![]() 和纵坐标
和纵坐标![]() ,并求
,并求![]() 与
与![]() 的关系式(不写
的关系式(不写![]() 的取值范围);
的取值范围);
(3)奥运组委会规定,运动员落地点距起跳点的水平距离为运动员本次跳跃的成绩,并且参赛的达标成绩为![]() .在运动员跳跃的过程中,点
.在运动员跳跃的过程中,点![]() 处有一个摄像头,记录运动员的空中姿态,当运动员飞过点
处有一个摄像头,记录运动员的空中姿态,当运动员飞过点![]() 时,在点
时,在点![]() 上方可被摄像头抓拍到.若运动员本次跳跃达到达标成绩,并且能被
上方可被摄像头抓拍到.若运动员本次跳跃达到达标成绩,并且能被![]() 处摄像头抓拍,求从点
处摄像头抓拍,求从点![]() 起跳后的水平速度
起跳后的水平速度![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
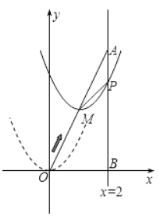
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连结
,连结![]() ,抛物线
,抛物线![]() 沿射线
沿射线![]() 方向平移得到抛物线
方向平移得到抛物线![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,设抛物线
,设抛物线![]() 的顶点
的顶点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线![]() 的解析式(用含
的解析式(用含![]() 的式子表示);
的式子表示);
(2)连结![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)点![]() 为
为![]() 轴上的动点,以
轴上的动点,以![]() 为直角顶点的
为直角顶点的![]() 与
与![]() 相似,求
相似,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
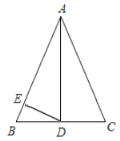
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 的外接圆与边
的外接圆与边![]() 交于点
交于点![]() ,
,![]() ,
,
(1)①补全图形;②判断直线![]() 与
与![]() 的外接圆的公共点个数,并给出证明.
的外接圆的公共点个数,并给出证明.
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]()
![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 轴交抛物线于点
轴交抛物线于点![]() .
.
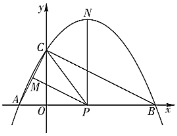
(1)求二次函数![]() 的解析式;
的解析式;
(2)①当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
②求![]() 的最大值;
的最大值;
(3)直接写出当![]() 面积最大时,点
面积最大时,点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com