
【题目】抛物线![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )经过点
)经过点![]() 和
和![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() 随着
随着![]() 的增大而减小.下列结论:①
的增大而减小.下列结论:①![]() ;②若点
;②若点![]() ,点
,点![]() 都在抛物线上,则
都在抛物线上,则![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.1个B.2个C.3个D.4个
【答案】B
【解析】
利用x<-1时,y随着x的增大而减小可判断抛物线开口向上,则a>0,由于抛物线经过点(-1,0)和(m,0),且1<m<2,可判断抛物线的对称轴的位置,所以![]() ,于是可对①进行判断;
,于是可对①进行判断;
通过比较点A到对称轴的距离和点B到对称轴的距离可对②进行判断;
根据二次函数图象上点的坐标特征得到a-b+c=0,am2+bm+c=0,消去c,再因式分解得到(m+1)(m-1)+b(m-1)=0,于是可对③进行判断;
利用抛物线顶点的纵坐标小于-1得到![]() ,然后利用不等式性质变形后可对④进行判断.
,然后利用不等式性质变形后可对④进行判断.
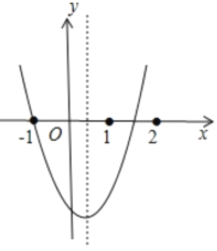
∵抛物线过点![]() ,当
,当![]() 时,
时,![]() 随着
随着![]() 的增大而减小,
的增大而减小,
∴抛物线开口向上.∴![]() .
.
∵抛物线经过点![]() 和
和![]() ,且
,且![]() ,
,
∴![]() .∴
.∴![]() .故①正确;
.故①正确;
∵点![]() ,点
,点![]() 都在抛物线上,而点
都在抛物线上,而点![]() 到对称轴的距离比点
到对称轴的距离比点![]() 到对称轴
到对称轴
的距离要大,
∴![]() .故②错误;
.故②错误;
∵抛物线经过点![]() 和
和![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .故③正确;
.故③正确;
∵![]() ,∴
,∴![]() .又
.又![]() ,
,
∴![]() .故④错误.
.故④错误.
故选B.


科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
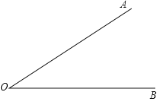
【题目】下面是小华设计的“作一个角等于已知角的2倍”的尺规作图过程.
已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如图,
①在射线![]() 上任取一点
上任取一点![]() ;
;
②作线段![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;
;
③连接![]() ;
;
所以![]() 即为所求作的角.
即为所求作的角.
根据小华设计的尺规作图过程,
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明(说明:括号里填写推理的依据).
证明:∵![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() ______(______)
______(______)
∴![]() .
.
∵![]() (______)
(______)
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点O的抛物线![]() (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
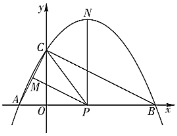
【题目】如图,已知二次函数![]()
![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 轴交抛物线于点
轴交抛物线于点![]() .
.
(1)求二次函数![]() 的解析式;
的解析式;
(2)①当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
②求![]() 的最大值;
的最大值;
(3)直接写出当![]() 面积最大时,点
面积最大时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营一批进价为2元的小商品,在市场营销中发现日销售单价x元与日销售量y件有如下关系:
x | 3 | 5 | 9 | 11 |
y | 18 | 14 | 6 | 2 |
(1)预测此商品日销售单价为11.5元时的日销售量;
(2)设经营此商品日销售利润(不考虑其他因素)为P元,根据销售规律,试求日销售利润P元与销售单价x元之间的函数关系式,问日销售利润P是否存在最大值或最小值?若有,试求出;若无,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
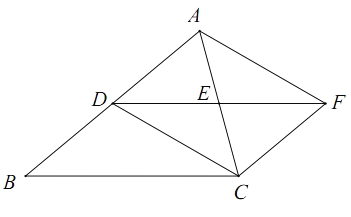
【题目】如图,在△ABC中,D为AB中点,过点D作DF//BC交AC于点E,且DE=EF,连接AF,CF,CD.
(1)求证:四边形ADCF为平行四边形;
(2)若∠ACD=45°,∠EDC=30°,BC=4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、E在⊙O上,∠B=2∠ACE,在BA的延长线上有一点P,使得∠P=∠BAC,弦CE交AB于点F,连接AE.
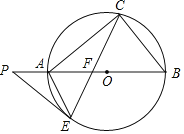
(1)求证:PE是⊙O的切线;
(2)若AF=2,AE=EF=![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com