
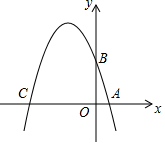
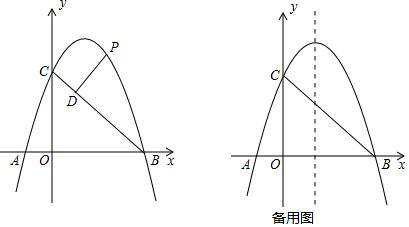
 如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.分析 (1)利用待定系数法求二次函数的解析式;
(2)当BP=AC且BP∥AC时,四边形ACBP为菱形,根据BP=AC=5,且点P到x轴距离等于OB,则点P的坐标为(5,3),且当点P在第二、三象限时,以A、B、C、P为顶点的四边形只能是平行四边形,不是菱形;
(3)求直线PA的解析式为:y=$\frac{3}{4}x-\frac{3}{4}$,当M与P、A两点不在同一直线上时,根据三角形三边关系的得|PM-AM|<PA.当点M与P、A两点在同一直线上时,得|PM-AM|=PA,则当点M与P、A两点在同一直线上时.|PM-AM|的值最大,此时点M为直线PA与抛物线的交点,列方程组解出即可.
解答 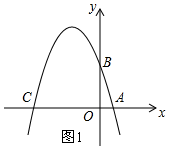 解:(1)∵OA=1,OB=3,OC=4.
解:(1)∵OA=1,OB=3,OC=4.
∴A(1,0),B(0,3),C(-4,0),
设抛物线的解析式为:y=a(x-1)(x+4),
把(0,3)代入得:3=-4a,
a=-$\frac{3}{4}$,
∴y=-$\frac{3}{4}$(x-1)(x+4),
∴抛物线的解析式为:y=-$\frac{3}{4}{x}^{2}-\frac{9}{4}$x+3;
(2)在平面直角坐标系xOy中存在一点P,使得A、B、C、P为顶点的四边形为菱形,
理由:∵OB=3,OC=4,OA=1,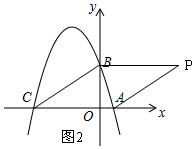
∴BC=AC=5,
当BP=AC且BP∥AC时,四边形ACBP为菱形,
∴BP=AC=5,且点P到x轴距离等于OB,
∴点P的坐标为(5,3),如图2,
当点P在第二、三象限时,以A、B、C、P为顶点的四边形只能是平行四边形,不是菱形,
∴当点P的坐标为(5,3)时,以A、B、C、P为顶点的四边形是菱形;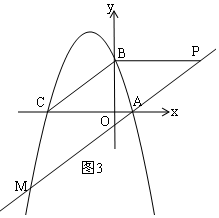
(3)设直线PA的解析式为y=kx+b(k≠0),
∴点A的坐标为(1,0)点P的坐标为(5,3),
则$\left\{\begin{array}{l}{k+b=0}\\{5k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-\frac{3}{4}}\end{array}\right.$,
∴直线PA的解析式为:y=$\frac{3}{4}x-\frac{3}{4}$,
当M与P、A两点不在同一直线上时,根据三角形三边关系的得|PM-AM|<PA.当点M与P、A两点在同一直线上时,得|PM-AM|=PA,
∴如图3,当点M与P、A两点在同一直线上时.|PM-AM|的值最大,此时点M为直线PA与抛物线的交点,
联立 $\left\{\begin{array}{l}{y=-\frac{3}{4}x-\frac{3}{4}}\\{y=-\frac{3}{4}{x}^{2}-\frac{9}{4}x+3}\end{array}\right.$ 解得 $\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-5}\\{{y}_{2}=-\frac{9}{2}}\end{array}\right.$,
∴当点M的坐标为(1,0)或(-5,-$\frac{9}{2}$)时,|PM-AM|的值最大,最大值是5.
点评 本题是二次函数的综合题,考查了利用待定系数法求二次函数和一次函数的解析式、菱形的性质和判定、三角形三边关系、两函数的交点问题以及两线段差的最值问题,第三问将两线段差的绝对值的最值问题转化为三角形的三边关系,使问题得以解决.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
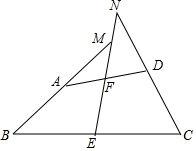 如图,在四边形ABCD中,AB=CD,点E、F分别是BC、AD的中点,连结EF并延长分别与BA、CD的延长线交于点M、N,∠BME与∠CNE的大小关系如何?试说明理由.
如图,在四边形ABCD中,AB=CD,点E、F分别是BC、AD的中点,连结EF并延长分别与BA、CD的延长线交于点M、N,∠BME与∠CNE的大小关系如何?试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
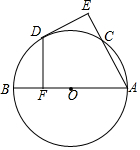 如图,AB为⊙O的直径,C为⊙O上一点,点D是弧BC的中点,DE⊥AC于点E,DE⊥AB于点F.
如图,AB为⊙O的直径,C为⊙O上一点,点D是弧BC的中点,DE⊥AC于点E,DE⊥AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com