
如图,⊙O经过菱形ABCD的三个顶点A、C、D,且与AB相切于点A.
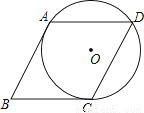
(1)求证:BC为⊙O的切线;
(2)求∠B的度数.
(1)证明见试题解析;(2)60°.
【解析】
试题分析:(1)连结OA、OB、OC、BD,根据切线的性质得OA⊥AB,即∠OAB=90°,再根据菱形的性质得BA=BC,然后根据“SSS”可判断△ABO≌△CBO,则∠BCO=∠BAO=90°,于是可根据切线的判定方法即可得到结论;
(2)由△ABO≌△CBO得∠AOB=∠COB,则∠AOB=∠COB,由于菱形的对角线平分对角,所以点O在BD上,利用三角形外角性质有∠BOC=∠ODC+∠OCD,则∠BOC=2∠ODC,
由于CB=CD,则∠OBC=∠ODC,所以∠BOC=2∠OBC,根据∠BOC+∠OBC=90°可计算出∠OBC=30°,然后利用∠ABC=2∠OBC计算即可.
解答:(1)证明:连结OA、OB、OC、BD,如图,
∵AB与⊙O切于A点,∴OA⊥AB,即∠OAB=90°,
∵四边形ABCD为菱形,∴BA=BC,
在△ABO和△CBO中,
∵AB=CB,OA=OC,OB=OB,∴△ABO≌△CBO(SSS),∴∠BCO=∠BAO=90°,∴OC⊥BC,
∴BC为⊙O的切线;
(2)【解析】
∵△ABO≌△CBO,∴∠ABO=∠CBO,
∵四边形ABCD为菱形,∴BD平分∠ABC,DA=DC,∴点O在BD上,
∵∠BOC=∠ODC+∠OCD,而OD=OC,∴∠ODC=∠OCD,∴∠BOC=2∠ODC,
而CB=CD,∴∠OBC=∠ODC,∴∠BOC=2∠OBC,
∵∠BOC+∠OBC=90°,∴∠OBC=30°,∴∠ABC=2∠OBC=60°.

考点:1.切线的判定与性质;2.菱形的性质.


科目:初中数学 来源:2014-2015学年江苏省盐城东台苏东双语九年级上学期第一次质量检测数学试卷(解析版) 题型:选择题
一元二次方程x2+x-1=0 的根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次模拟数学试卷(解析版) 题型:选择题
下列说法中不一定正确的是( )
A.所有等腰直角三角形都相似
B.所有矩形相似
C.所有等边三角形相似
D.直角三角形被斜边上的高分成的两个三角形相似
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次模拟数学试卷(解析版) 题型:选择题
已知一组数据2,1,x,7,3,5,3,2 的众数是2,则这组数据的中位数是( )
A.2 B.2.5 C.3 D.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,已知点A、B、C的坐标分别为(0,0),(4,0),(5, 2)将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.
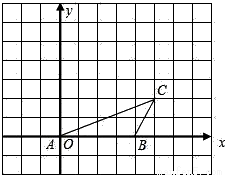
(1)画出△AB′C′;
(2)求点C′的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,已知AB为⊙O的直径,点C在⊙O上,∠C=15°,则∠BOC的度数为________________.
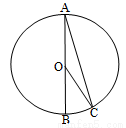
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏东台苏东双语八年级上学期第一次质检数学试卷(解析版) 题型:解答题
已知,如图,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点。
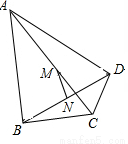
求证:①BM=DM ②MN⊥BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com