【题目】已知一次函数的图象经过点P（0，－2），且与两条坐标轴截得的直角三角形的面积为6，求这个一次函数的解析式．
【答案】y=-
x-2或y=x-2．
【解析】
分一次函数与x轴交点Q在正半轴与负半轴两种情况确定出Q的坐标，即可确定出一次函数解析式．
解：设一次函数与x轴的交点为Q,则
①当一次函数与x轴交点Q在x轴负半轴时，
由OP=2，与两坐标所围成的直角三角形面积为6，得到Q（-6，0），
设一次函数解析式为y=kx+b，将P与Q坐标代入得：
解得
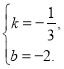
此时一次函数解析式为y=-x-2；
②当一次函数与x轴交点在x轴正半轴时，
由OP=2，与两坐标所围成的直角三角形面积为6，得到Q（6，0），
设一次函数解析式为y=mx+n，将P与Q坐标代入得：
解得
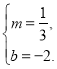
此时一次函数解析式为y=x-2．
故所求一次函数解析式为：y=-x-2或y=x-2．
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，OA=OB，AC=CD，已知两点A(4，0)，C(0，7)，点D在第一象限内，∠DCA=90°，点B在线段OC上，AB的延长线与DC的延长线交于点M，AC与BD交于点N.
（1）点B的坐标为： ；
（2）求点D的坐标；
（3）求证：CM=CN.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝8，AC＝5，AD是∠BAC的角平分线，点D在△ABC内部，连接AD、BD、CD，∠ADB＝150°，∠DBC＝30°，∠ABC+∠ADC＝180°，则线段CD的长度为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下面四个结论：①OA＝OD；②AD⊥EF；③当∠BAC＝90°时，四边形AEDF是正方形；④AE2＋DF2＝AF2＋DE2.其中正确的是_________．(填序号)
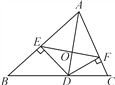
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙、丙3名学生各自随机选择到A、B 2个书店购书.
（1）求甲、乙2名学生在不同书店购书的概率；
（2）求甲、乙、丙3名学生在同一书店购书的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，□ABCD的对角线AC，BD相交于点O，E、F、G、H分别是OA、OB、OC、OD的中点，那么□ABCD与四边形EFGH是否是位似图形？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，对角线AC，BD相交于点O，AB=5，AC=6，BD=8．
（1）求证：四边形ABCD是菱形；
（2）过点A作AH⊥BC于点H，求AH的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
