
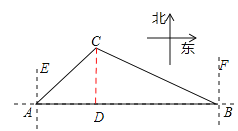
【题目】如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.
(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);
(2)求海轮在B处时与灯塔C的距离(结果保留整数).
(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)

【答案】(1)海轮在航行过程中与灯塔C的最短距离是34.4海里;
(2)海轮在B处时与灯塔C的距离约为60海里.
【解析】试题分析:(1)过点C作CD⊥AB于点D,则CD的长为海轮在航行过程中与灯塔C的最短距离.
(2)在Rt△BCD中,根据55°角的余弦值即可求出海轮在B处时与灯塔C的距离.
试题解析:解:(1)如答图,过点C作CD⊥AB于点D,
依题意得:∠ACD=∠CAE=42°,∠BCD=∠CBF=55°,
设CD的长为x海里,
在Rt△ACD中,tan42°=![]() ,则AD=xtan42°,
,则AD=xtan42°,
在Rt△BCD中,tan55°=![]() ,则BD=xtan55°,
,则BD=xtan55°,
∵AB=80,∴AD+BD="80." ∴xtan42°+xtan55°=80,解得:x≈34.4.
答:海轮在航行过程中与灯塔C的最短距离是34.4海里.
(2)在Rt△BCD中,cos55°=![]() ,∴BC=
,∴BC=![]() ≈60海里.
≈60海里.
答:海轮在B处时与灯塔C的距离是60海里.


科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著 .是《算经十书》中最重要的一部,成于公元一世纪左右 .全书总结了战国、秦、汉时期的数学成就 .同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,其中有一个数学问题“今有垣厚一丈,两鼠对穿 .大鼠日一尺,小鼠亦一尺 .大鼠日自倍,小鼠日自半 .问:何日相逢?”.译文:“有一堵一丈(旧制长度单位,1丈=10尺=100寸)厚的墙,两只老鼠从两边向中间打洞 .大老鼠第一天打一尺,小老鼠也是一尺 .大老鼠每天的打洞进度是前一天的一倍,小老鼠每天的进度是前一天的一半 .问它们几天可以相逢?”请你用所学数学知识方法给出答案:______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
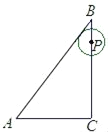
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P以每秒一个单位的速度沿着B﹣C﹣A运动,⊙P始终与AB相切,设点P运动的时间为t,⊙P的面积为y,则y与t之间的函数关系图象大致是( )
A. 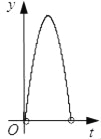 B.
B. 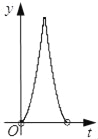 C.
C. 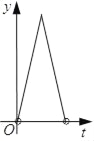 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心![]() 出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段
出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段![]() 、(2)半圆弧
、(2)半圆弧![]() 、(3)线段
、(3)线段![]() 后,回到出发点.蚂蚁离出发点的距离
后,回到出发点.蚂蚁离出发点的距离![]() (蚂蚁所在位置与
(蚂蚁所在位置与![]() 点之间线段的长度)与时间
点之间线段的长度)与时间![]() 之间的图象如图2所示,问:(注:圆周率
之间的图象如图2所示,问:(注:圆周率![]() 的值取3)
的值取3)
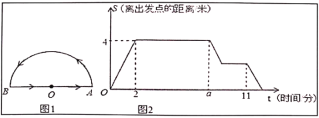
(1)请直接写出:花坛的半径是 米,![]() .
.
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回![]() 所用时间.
所用时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
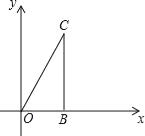
【题目】已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=![]() ,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.
,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
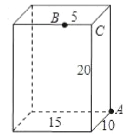
【题目】如图,长方形的长为15,宽为10,高为20,点![]() 离点
离点![]() 的距离为5,蚂蚁如果要沿着长方形的表面从点
的距离为5,蚂蚁如果要沿着长方形的表面从点![]() 爬到点
爬到点![]() ,需要爬行的最短距离是( )
,需要爬行的最短距离是( )
A.35B.![]() C.25D.
C.25D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1<![]() <2,所以
<2,所以![]() 的整数部分为1,将
的整数部分为1,将![]() 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分![]() ,根据以上的内容,解答下面的问题:
,根据以上的内容,解答下面的问题:
(1)![]() 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;
(2)![]() 的整数部分是______,小数部分是_____;
的整数部分是______,小数部分是_____;
(3)若设![]() 整数部分是x,小数部分是y,求x﹣
整数部分是x,小数部分是y,求x﹣![]() y的值.
y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某油脂公司生产销售菜籽油、花生油两种食用植物油.
(1)已知花生的出油率为56%,是菜籽的1.4倍,现有菜籽、花生共100吨,若想得到至少52吨植物油,则其中的菜籽至多有多少吨?
(2)在去年的销售中,菜籽油、花生油的售价分别为20元/升,30元/升,且销量相同,今年由于花生原材料价格上涨,花生油的售价比去年提高了a%,菜籽油的售价不变,总销量比去年降低a%,且菜籽油、花生油的销量均占今年总销量的![]() ,这样,预计今年的销售总额比去年下降
,这样,预计今年的销售总额比去年下降![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com