解:(1)设直线BC的解析式为:y=kx+b,
∵点B、点C坐标分别为(8,0)、(0,-4).
∴
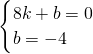
,
解得:

,
故过B、C两点的一次函数解析式为:y=

x-4:
(2)设P的坐标为:(x,

x-4),
∵点A、点C坐标分别为(4,0)、(0,-4).
∴OA=OC=4,
∵以点O、A、P为顶点的三角形面积和以点O、C、P为顶点的三角形面积相等,
∴|

x-4|=|x|,
即

x-4=x或

x-4=-x,
解得:x=-8或x=

,
故P的坐标为:(-8.-8)或(

,-

);
(3)连接AC,
∵OA=OC=4,
∴AC=
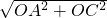
=4

,
①若AQ=CQ,则点Q
1(0,0);
②若AQ=AC,则点Q
2(0,4);
③若CQ=AC=4

,则Q
3(0,4

-4)或Q
4(0,-4

-4);
综上可得:点Q的坐标分别为:(0,0)、(0,4)、(0,4

-4)、(0,-4

-4).
分析:(1)首先设直线BC的解析式为:y=kx+b,由点B、点C坐标分别为(8,0)、(0,-4).利用待定系数法即可求得过B、C两点的一次函数解析式;
(2)由以点O、A、P为顶点的三角形面积和以点O、C、P为顶点的三角形面积相等,OA=OC,可得点P的横坐标与纵坐标的绝对值相等,即可求得P点坐标;
(3)分别从AQ=CQ,AQ=AC,CQ=AC去分析求解即可求得答案.
点评:此题考查了待定系数法求一次函数的解析式、等腰三角形的性质以及三角形面积问题.此题难度较大,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

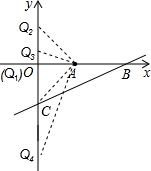
 在直角坐标系XOY中,点A、点B、点C坐标分别为(4,0)、(8,0)、(0,-4).
在直角坐标系XOY中,点A、点B、点C坐标分别为(4,0)、(8,0)、(0,-4).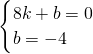 ,
, ,
, x-4:
x-4: x-4),
x-4), x-4|=|x|,
x-4|=|x|, x-4=x或
x-4=x或 x-4=-x,
x-4=-x, ,
, 故P的坐标为:(-8.-8)或(
故P的坐标为:(-8.-8)或( ,-
,- );
);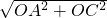 =4
=4 ,
, ,则Q3(0,4
,则Q3(0,4 -4)或Q4(0,-4
-4)或Q4(0,-4 -4);
-4); -4)、(0,-4
-4)、(0,-4 -4).
-4).


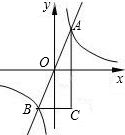 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.