
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1︰5,则  的值为( ).
的值为( ).

A.2 B.4 C. D.
D.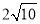
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:选择题
在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A.11+ B.11﹣
B.11﹣ C.11+
C.11+ 或11﹣
或11﹣ D.11+
D.11+ 或1+
或1+
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题四数学试卷(解析版) 题型:填空题
为了中考“跳绳”项目能得到满分,小明练习了6次跳绳,每次跳绳的个数如下(单位:个):176, 183, 187,179,187,188.这6次数据的中位数是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:解答题
如图,在□ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME.
(1)若AM=2AE=4,∠BCE=30°,求□ABCD的面积;
(2)若BC=2AB,求证:∠EMD=3∠MEA.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:填空题
将长度为12厘米的线段截成两条线段a、b(a、b长度均为整数).如果截成的a、b长度分别相同算作同一种截法(如:a=9,b=1和a=1,b=9为同一种截法),那么以截成的a、b为对角线,以另一条c=4厘米长的线段为一边,能构成平行四边形的概率是__________.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:选择题
某人骑车沿直线旅行,先前进了 千米,休息了一段时间,又原路原速返回了
千米,休息了一段时间,又原路原速返回了 千米(
千米( ),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离
),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离 与时间
与时间 的函数关系的大致图象是( ).
的函数关系的大致图象是( ).

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题三数学试卷(解析版) 题型:解答题
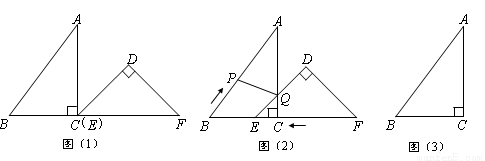
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm。
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动。当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移。DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5)。解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由。
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由。(图(3)供同学们做题使用)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题三数学试卷(解析版) 题型:选择题
如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )。
A.25° B.30° C.40° D.50°

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级下学期期中考试数学试卷(解析版) 题型:解答题
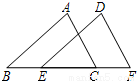
如图,已知点E、C在线段BF上,BE=CF,AB∥DE,AB=DE.
求证:AC∥DF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com